Bài viết này HOCMAI sẽ gửi đến các bạn học sinh các dạng bài tập hình cầu. Bao gồm tính diện tích hình cầu và mặt cầu, thể tích hình cầu theo cấp độ từ cơ bản đến nâng cao kèm lời giải chi tiết. Từ đó giúp các bạn học sinh môn Toán lớp 9 nắm vững kiến thức và cách giải các dạng bài tập về hình cầu một cách dễ dàng.
Bạn nên tham khảo một số bài viết liên quan:
I. Tổng quan kiến thức về hình cầu
Trong đời sống thường ngày, hình cầu là hình dạng được ứng dụng phổ phiến. Bạn có thể nhìn thấy các đồ vật có dạng hình cầu như: viên bi, quả bóng tennis, quả cầu pha lê,…
Khái niệm hình cầu
Trong toán học, hình cầu được giải thích là hình được tạo ra khi xoay nửa hình tròn một vòng quanh đường kính của của nó. Khi đó tâm và bán kính của hình tròn chính là tâm và bán kính hình cầu đó.
Khái niệm mặt cầu
Tập hợp tất cả các điểm cách đều tâm O của hình cầu với khoảng cách không đổi bằng R (bán kính) được gọi là mặt cầu.
Công thức tính diện tích hình cầu
S=4πR^2 | S=πd^2
Trong đó:
- S là diện tích hình cầu
- π là hằng số Pi, xấp xỉ bằng 3,14
- R là bán kính hình cầu
- d là đường kính hình cầu
Công thức tính thể tích hình cầu
V = 4/3ΠR^3
Trong đó:
- V là thể tích hình cầu
- π là hằng số Pi, xấp xỉ bằng 3,14
- R là bán kính hình cầu
II. Bài tập về hình cầu – Tính diện tích, thể tích kèm lời giải
Bài 1: Một hình cầu có đường kính bằng 6cm. Vậy mặt cầu có diện tích là:
A. 6π (cm2)
B. 36π (cm2)
C. 18π (cm2)
D. 72π (cm2)
Hướng dẫn giải
Theo đề bài ra, ta có d = 6cm. Áp dụng công thức tính diện tích mặt cầu ta có:
Diện tích mặt cầu: S = πd^2 = π x 6^2 = 36π (cm2)
Vậy B chính là đáp án chính xác
Bài 2: Một mặt cầu có thể tích bằng 288π (cm3). Đường kính của mặt cầu là:
A. 12 cm
B. 2 cm
C. 16 cm
D. 6 cm
Hướng dẫn giải
Theo đề bài ra, ta có V = 288π (cm3). Áp dụng công thức tính thể tích mặt cầu ta có:
V = 4/3ΠR^3 = 288π => R = 6
Từ đó đường kính của mặt cầu là: d = 2R = 2 x 6 = 12 cm
Vậy A chính là đáp án chính xác
Bài 3: Cho mặt cầu có số đo thể tích bằng số đo diện tích. Tìm bán kính mặt cầu đó:
- 9
- 3
- 18
- 6
Hướng dẫn giải
Theo giả thuyết của đề bài, ta có S = V:
=> 4πR^2 = 4/3ΠR^3 => 3R^2 = R^3 => R = 3 cm
Vậy B chính là đáp án chính xác
Bài 4: Một hình cầu có R = 3cm và một hình nón cũng có r đáy = 3cm và có diện tích toàn phần bằng diện tích mặt cầu. Tìm chiều cao của hình nón đó?
A. 3√3
B. 2√6
C. 6√2
D. 6
Hướng dẫn giải
Gọi l là đường sinh của hình nón. Theo đề bài, vì diện tích toàn phần của hình nón bằng diện tích mặt cầu và r = R = 3cm nên ta sẽ có:
4πR^2 = π.R.l + π.R^2 ⇔ 4R^2 = R.l + R^2 ⇔ 3R^2 = R.l=> l = 3R = 3 x 3 = 9 (cm)
Áp dụng công thức tính đường cao của hình nón, ta có:
h^2= l^2 – r^2 = 9^2 – 3^2 = 81 – 9 = 72 => h = 6√2 cm
Vậy C chính là đáp án chính xác
Bài 5: Một hình cầu có S mặt cầu = 64π (cm2). Tìm thể tích khối cầu đó?
A. 256π (cm3)
B. (64π)/3 (cm3)
C. (256π)/3 (cm3)
D. Đáp án khác
Hướng dẫn giải
Theo đề bài, ta có:
Diện tích mặt cầu: S = 4πR^2 = 64π ⇔ R^2 = 16 => R = 4cm
Vậy thể tích mặt cầu là: V = 4/3πR^3 = 4/3π x 4^3 = (256π)/3 (cm3)
Vậy C chính là đáp án chính xác
Bài 6: Một hình cầu có V = (500π)/3, Tìm V mặt cầu?
A. 150π (cm2)
B. 75π (cm2)
C. 125π (cm2)
D. 100π (cm2)
Hướng dẫn giải
Theo đề bài, ta có:
Thể tích mặt cầu: V = 4/3πR^3 = (500π)/3 ⇔ 4R^3 = 500 => R = 5cm
Vậy diện tích mặt cầu là: S = 4πR^2 = 4π x 5^2 = 100 (cm3)
Vậy D chính là đáp án chính xác
Bài 7: Một hình trụ có r đường tròn đáy = 3cm và h = 4cm. Một hình cầu có diện tích bằng diện tích xung quanh của hình trụ. Tìm bán kính của hình cầu đó?
- R = 2cm
- R = 6cm
- R = √2 cm
- R = √6 cm
Hướng dẫn giải
Theo đề bài, ta có:
Diện tích xung quanh hình trụ là: Sxq= 2πrh = 2π x 3 x 4 = 24π (cm2)
Vậy diện tích mặt cầu là: S = 4πR^2 = 24π => R^2 = 6 => R = √6 cm
Vậy D chính là đáp án chính xác
Bài 8: Một hình cầu nội tiếp bên trong hình trụ. Biết rằng chiều cao của hình trụ bằng ba lần bán kính đáy và bán kính đáy hình trụ bằng bán kính của hình cầu. Tìm tỉ số giữa thể tích hình cầu và thể tích hình trụ?
A. 4/9
B. 2/4
C. 4/3
D. 2
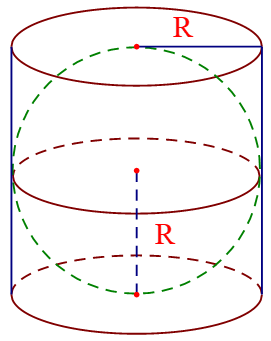
Hướng dẫn giải
Theo đề bài, ta có: H = 3R với R là bán kính cầu và cũng là bán kính của hình trụ.
- Thể tích hình cầu là: Vc = 4/3πR^3
- Thể tích khối trụ là: Vt = πR^2.3R = 3πR^3
Vậy tỉ số giữa thể tích hình cầu và thể tích hình trụ là:
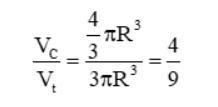
Vậy A chính là đáp án chính xác
Bài 9: Cho một hình lập phương ngoại tiếp với một hình cầu. Nếu diện tích toàn phần hình lập phương bằng 24cm2 thì diện tích mặt cầu là?
A. 2π
B. 2
C. 4
D. 4π
Hướng dẫn giải
Theo đề bài, vì hình lập phương ngoại tiếp hình cầu tiếp => bán kính hình cầu R = a/2 (với a là cạnh hình lập phương)
Diện tích toàn phần của hình lập phương là: Stp = 6a^2 = 24 => a^2 = 4cm => a = 2cm
Từ đó => r = a/2 = 1cm
Vậy diện tích mặt cầu là: Sc = 4πR^2 = 4π.1 = 4π (cm2)
Vậy D chính là đáp án chính xác
Bài 10: Cho tam giác ABC vuông cân tại A với cạnh góc vuông là a. Tính diện tích mặt cầu được tạo thành khi ta quay nửa đường tròn ngoại tiếp tam giác ABC một vòng xung quanh cạnh BC.
A. 2π.a^2 cm2
B. (π.a^2) / 2 cm2
C. a^2) / 2 cm2
D. π.a / 2 cm2
Hướng dẫn giải
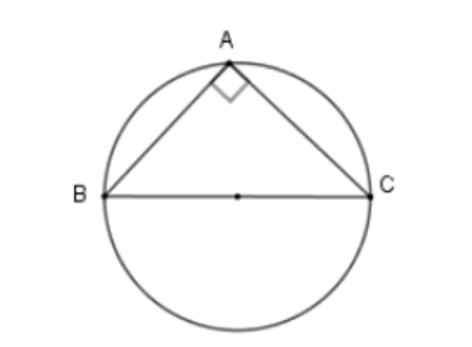
Theo đề bài, tam giác ABC vuông tại A và có đường tròn ngoại tiếp là đường tròn đường kính BC. Vậy bán kính đường tròn ngoại tiếp tam giác là: R = BC/2
Áp dụng định lý Pytago, ta có: BC^2 = AB^2 + AC^2 = 2a^2 => BC = a√2 => R = (a√2)/2
Diện tích mặt cầu được tạo thành khi ta quay nửa đường tròn ngoại tiếp tam giác ABC một vòng xung quanh cạnh BC là: S = 4πR^2 = 4π x ((a√2)/2)^2 = 2π.a^2 (cm2)
Vậy A chính là đáp án chính xác
(Hết)
Vừa rồi là bài viết các dạng bài tập hình cầu bao gồm tính diện tích hình cầu và mặt cầu, thể tích hình cầu theo cấp độ từ cơ bản đến nâng cao kèm lời giải chi tiết. Mong rằng bài viết sẽ giúp các bạn học sinh lớp 9 nắm vững kiến thức và vận dụng được để giải các dạng bài tập về hình cầu một cách dễ dàng.


















