Trong bài viết ngày hôm nay, HOCMAI xin được gửi đến các em học sinh những bài tập hình trụ. Ở trường, những bài toán về hình học không gian thường sẽ là thử thách đối với các em học sinh nói chung và các em đang học chương trình Toán 9 nói riêng vì chúng yêu cầu các em vừa có tư duy logic, vừa có óc tưởng tượng hình ảnh. Còn chần chừ gì nữa, các em hãy lấy giấy bút lên và cùng làm bài với HOCMAI ngay thôi nào!
Lý thuyết cơ bản về hình trụ
Khái niệm về hình trụ
Hình trụ là một hình học không gian cơ bản, được giới hạn bởi mặt trụ và hai đáy là hai đường tròn bằng nhau.
Tham khảo thêm kiến thức chi tiết về hình trụ, các em học sinh có thể tham khảo bài viết: Hình trụ là gì?
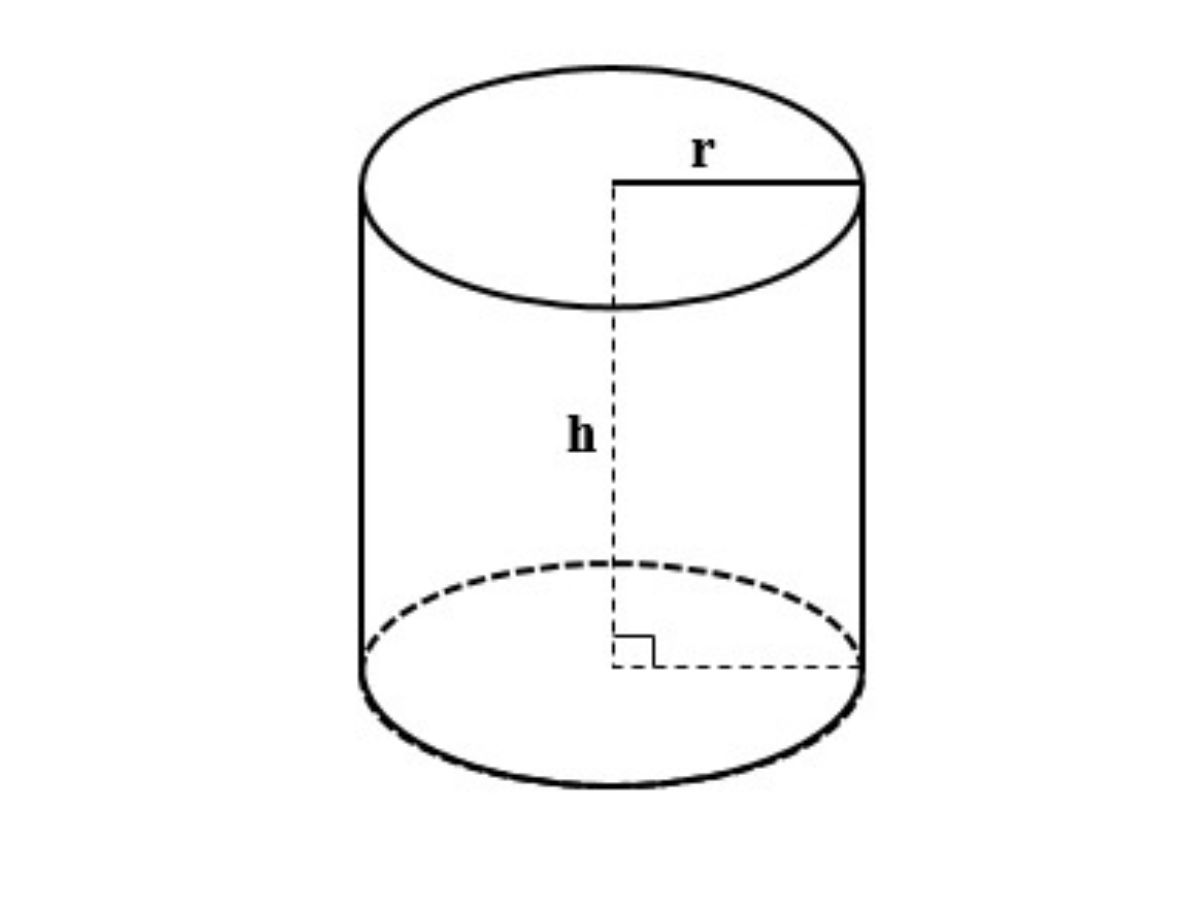
Công thức hình trụ:
Diện tích xung quanh:
Sxq = 2πr.h
Trong đó:
Sxq là diện tích xung quanh
2πr là chu vi đường tròn đáy
h là chiều cao của hình trụ
r là bán kính đường tròn đáy
Diện tích toàn phần:
Stp = 2.π.r.h + 2.π.r²
Trong đó:
Stp là diện tích toàn phần
2πrh là diện tích của hai đường tròn đáy
2πr² là diện tích xung quanh
Thể tích:
V = π.r².h
Trong đó:
V là thể tích hình trụ
Πr2 là diện tích đáy
h là chiều cao

Bài tập về hình trụ
Những bài tập hình trụ dưới đây đã được HOCMAI chắt lọc, sẽ bao gồm 2 phần là bài tập cơ bản và bài tập nâng cao. các em học sinh thực hành theo nhé!
Bài tập cơ bản về hình trụ
Bài 1: Cho khối trụ sau, với thiết diện qua trục là hình vuông cạnh 2a. Tính:
- diện tích xung quanh.
- diện tích toàn phần.
- thể tích của khối trụ.
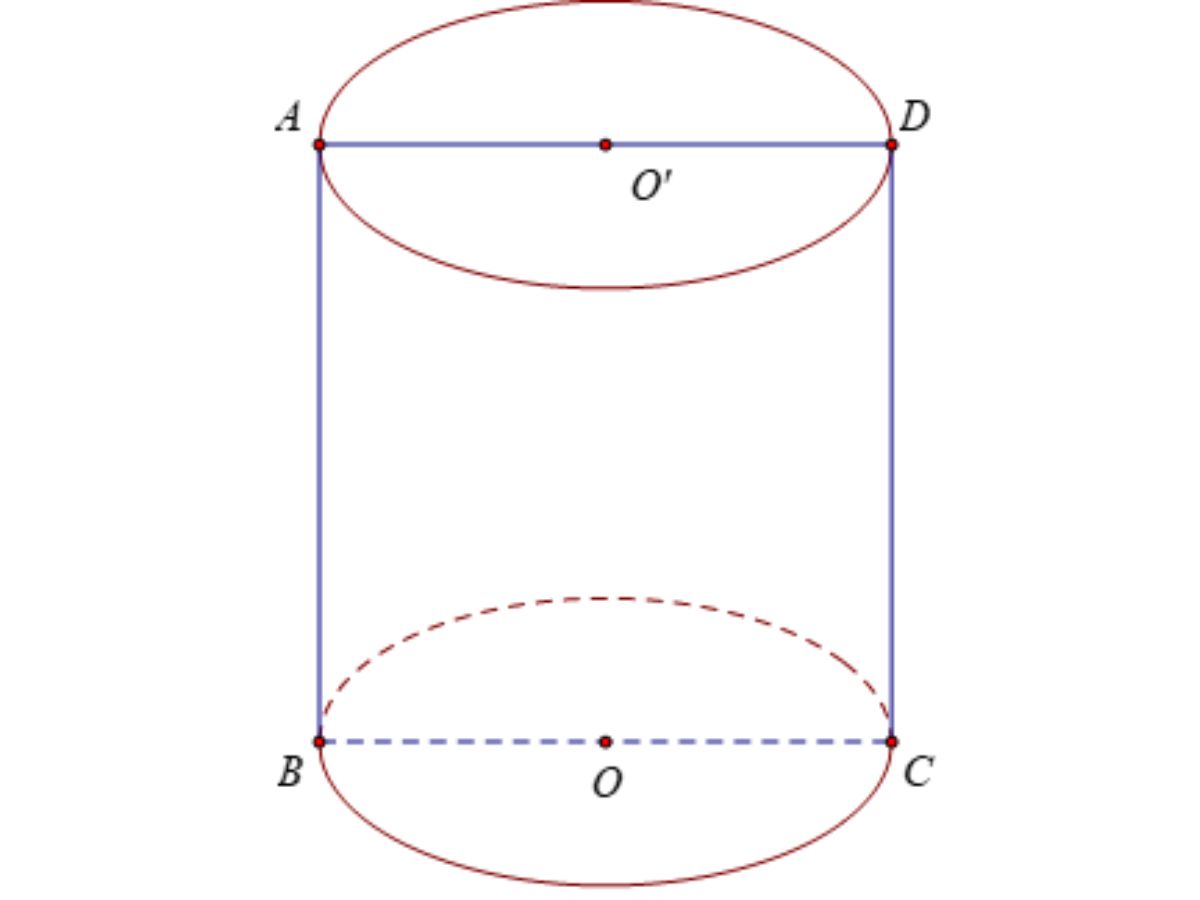
Hướng dẫn giải bài:
Thiết diện: hình vuông ABCD (với cạnh 2a)
Đường cao của hình trụ là AB = 2a, bán kính đáy là OB = a.
Diện tích xung quanh là: Sxq = 2πrh = 2π.a.2a = 4πa²
Diện tích toàn phần là: Stp = 2πrh+2πr² = 4πa²+2πa² = 6πa²
Thể tích là: V = πr²h = π.a².2a = 2πa³
Bài 2: Cho hình chữ nhật ABCD có AB = a và góc BDC = 30º . Quay hình chữ nhật quanh trục AD sẽ tạo thành một hình trụ (T). Hãy tính diện tích xung quanh của (T).
Hướng dẫn giải bài:
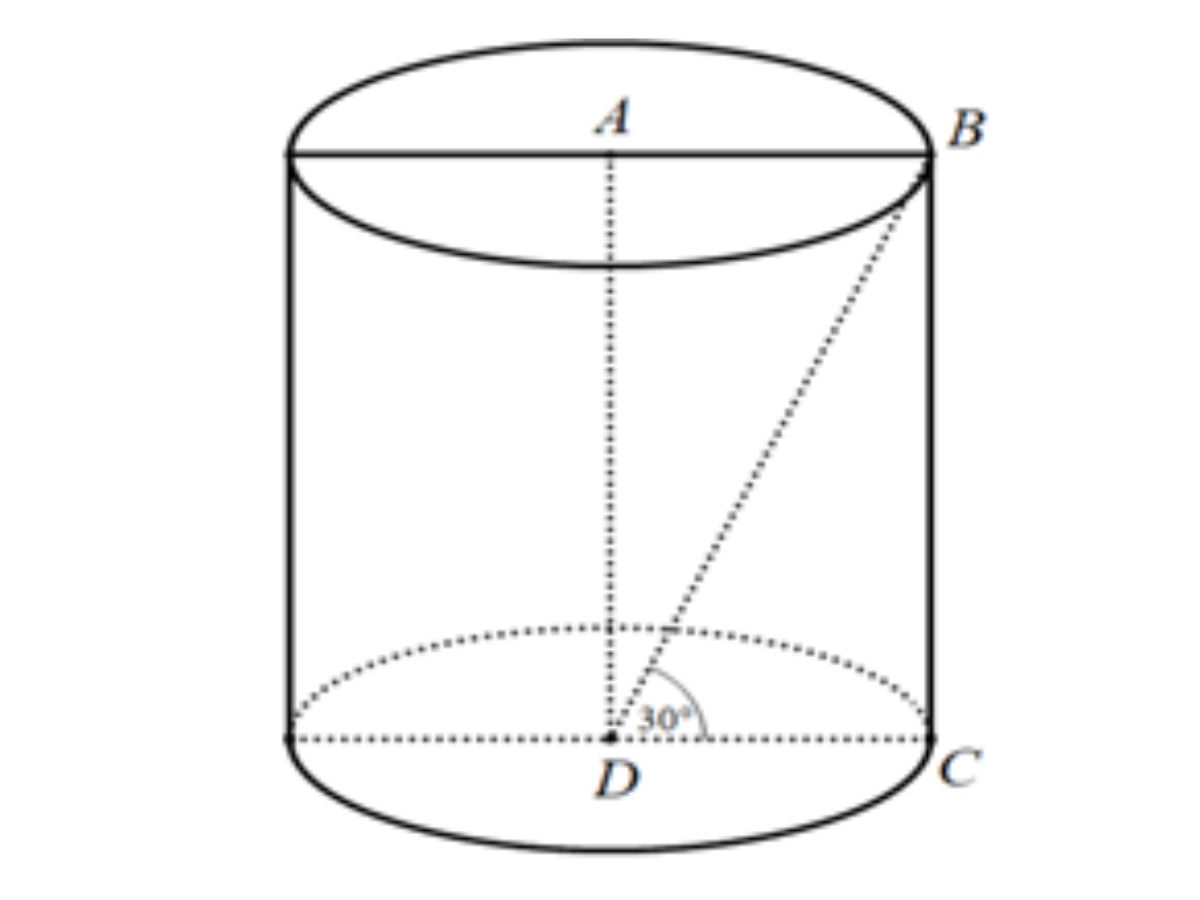
+ Khi quay một hình chữ nhật quanh cạnh AD, ta được một hình trụ như hình vẽ.
Hình trụ gồm có:
+ Bán kính đường tròn đáy: r = AB = a
+ Đường cao của hình trụ là:
h = BC = CD.tan300 = a.1/√3 = a/√3
Diện tích xung quanh cần tìm là:
Sxq = 2πrh = 2πa.a/√3 = 2πa²/√3
Bài 3: Một hình trụ có: r = 5 cm (bán kính đáy), h = 7cm (chiều cao). Tính:
- Diện tích xung quanh
- Diện tích toàn phần
- Thể tích của hình trụ
Hướng dẫn giải bài:
Diện tích xung quanh là: Sxq = 2πrh = 2π.5.7 = 70π
Diện tích toàn phần là: Stp = 2πrh + 2πr² = 70π+2π.5² = 120π
Thể tích là: V= πr²h = 2π.5².7 = 350π
Bài 4:
- a) Cho một hình trụ (T) có diện tích toàn phần là 120π (cm2) và bán kính đáy là 6 cm. Chiều cao của (T) là?
- b) Cho một hình trụ (T). Thể tích (T) bằng 81π (cm3) và đường sinh gấp ba lần bán kính đáy. Tính độ dài đường sinh của (T)
Hướng dẫn giải bài:
a) Ta có:
Stp = 2πrh + 2πr² = 2π.6.h + 2π.6² = 120π
⇒ h = 4(cm)
Vậy, chiều cao của (T) là 4 cm.
b) Gọi r là bán kính đáy của hình trụ
Do đường sinh và chiều cao bằng nhau nên chiều cao của hình trụ là 3r
Thể tích hình trụ: V = πr²h = πr².3r = 81π ⇒ r = 3
Suy ra độ dài đường sinh là 3.3 = 9 cm.
Bài tập nâng cao về hình trụ
Bài 1: Cho khối trụ có bán kính đáy R = a .Thiết diện song song với trục và cách trục khối trụ một khoảng bằng a/2, thiết diện đó là hình chữ nhật có diện tích bằng a²√3 .Tính thể tích của khối trụ.
Hướng dẫn giải bài:
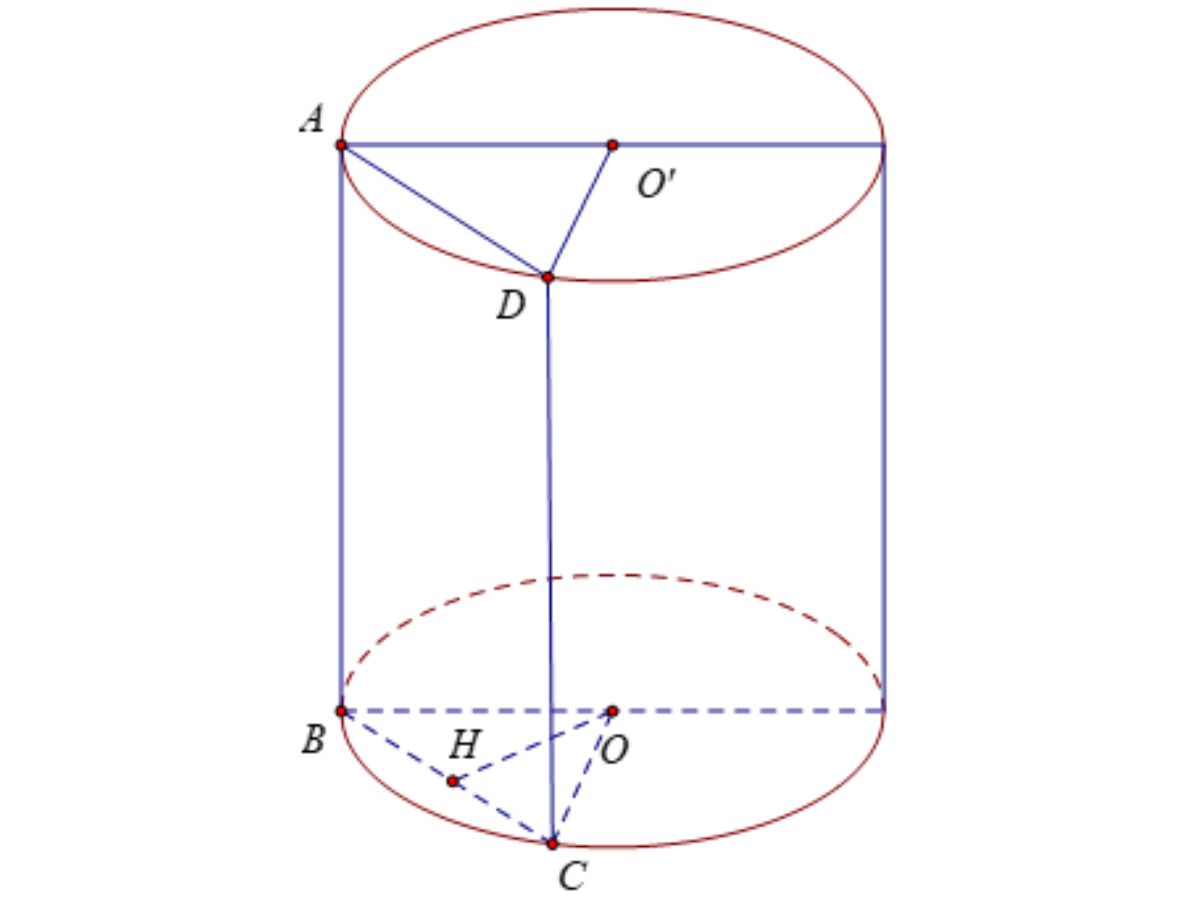
Tam giác BOC cân tại O với đường cao OH
⇒ H là trung điểm của BC
⇒ BC = 2BH = 2√(BO² – HO²)
⇒ 2√(a² – a²/4) = a√3
ABCD là hình chữ nhật nên:
SABCD = AB.BC=AB.a√3=a²√3⇒ AB=a
Thể tích của khối trụ là:
V = πr²h = π.a².a = πa³
Bài 2: Cho một khối trụ, cắt khối trụ đó bởi một mặt phẳng qua trục ta được thiết diện là hình chữ nhật ABCD , trong đó AB và CD thuộc hai đáy của khối trụ. Biết rằng AD = 12 cm và góc ACD bằng 60º. Tính thể tích của khối trụ.
Hướng dẫn giải bài:
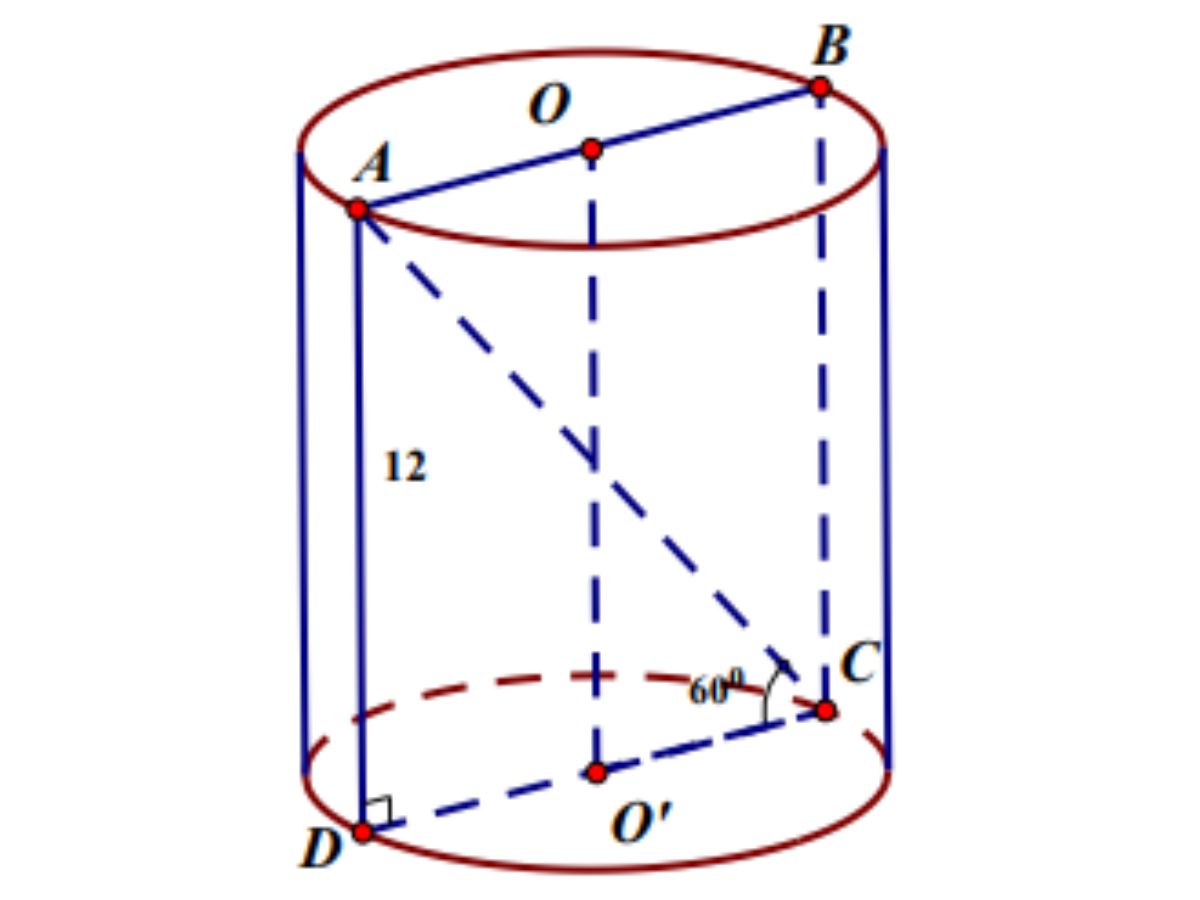
Xét tam giác ADC, góc C bằng 90° có:
CD = AD.cotACD
= 12.cot60° = 4√3
R = O’C = CD/2 = 2√3
Thể tích của khối trụ là:
V = πr²h = π.(2√3)².12 = 144π
Bài 3: Cho hình trụ có hai đáy là hình tròn (O) và (O’). Trên hai đường tròn lấy hai điểm A và B, sao cho AB và mặt phẳng chứa đường tròn đáy tạo ra một góc bằng 450 và khoảng cách đến trục OO’ bằng a√2/2. Biết bán kính đáy bằng a, tính thể tích của khối trụ theo a.
Hướng dẫn giải bài:
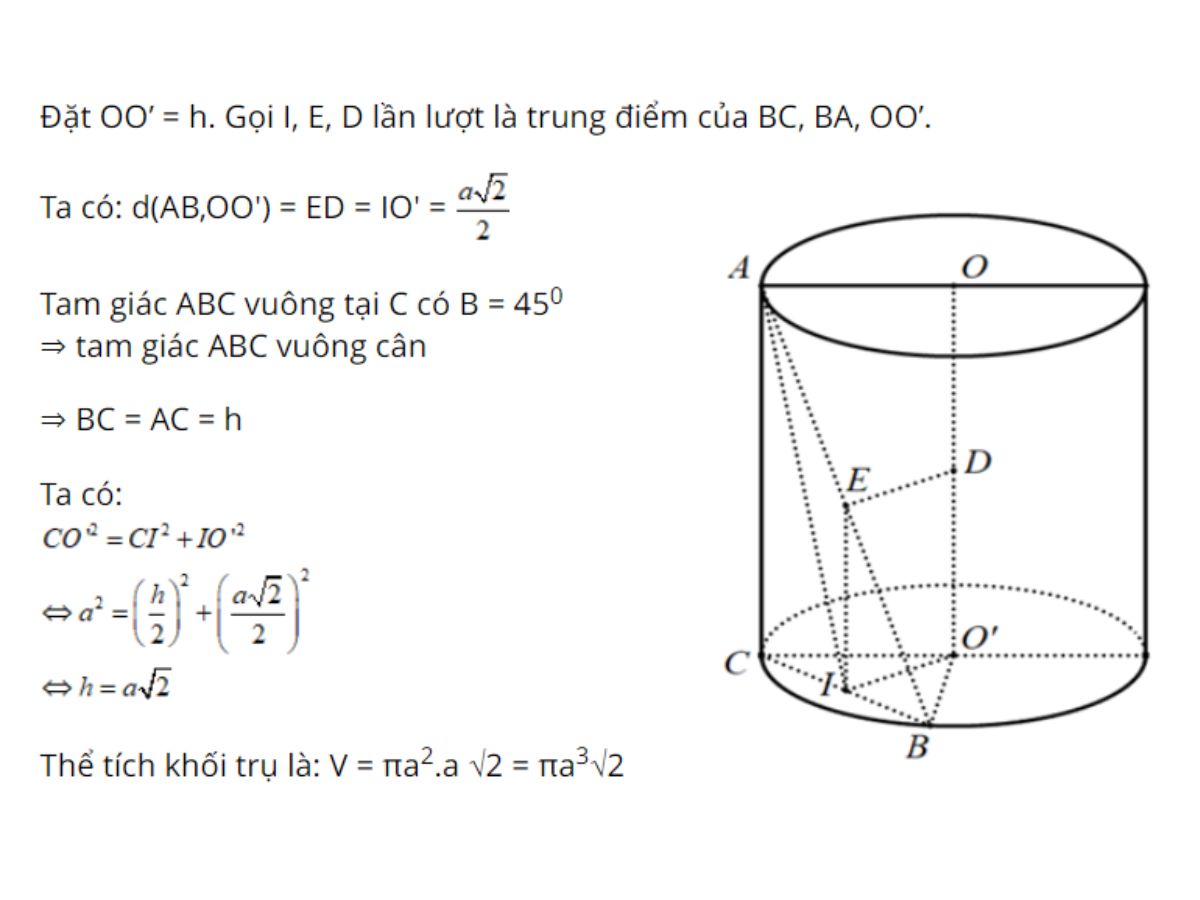
Bài 4: Cho ABCD là một hình tứ diện đều cạnh a. Xét hình trụ có 1 đáy là đường tròn nội tiếp tam giác ABC và có chiều cao bằng chiều cao hình tứ diện. Tìm diện tích xung quanh của hình trụ đó.
Hướng dẫn giải bài:
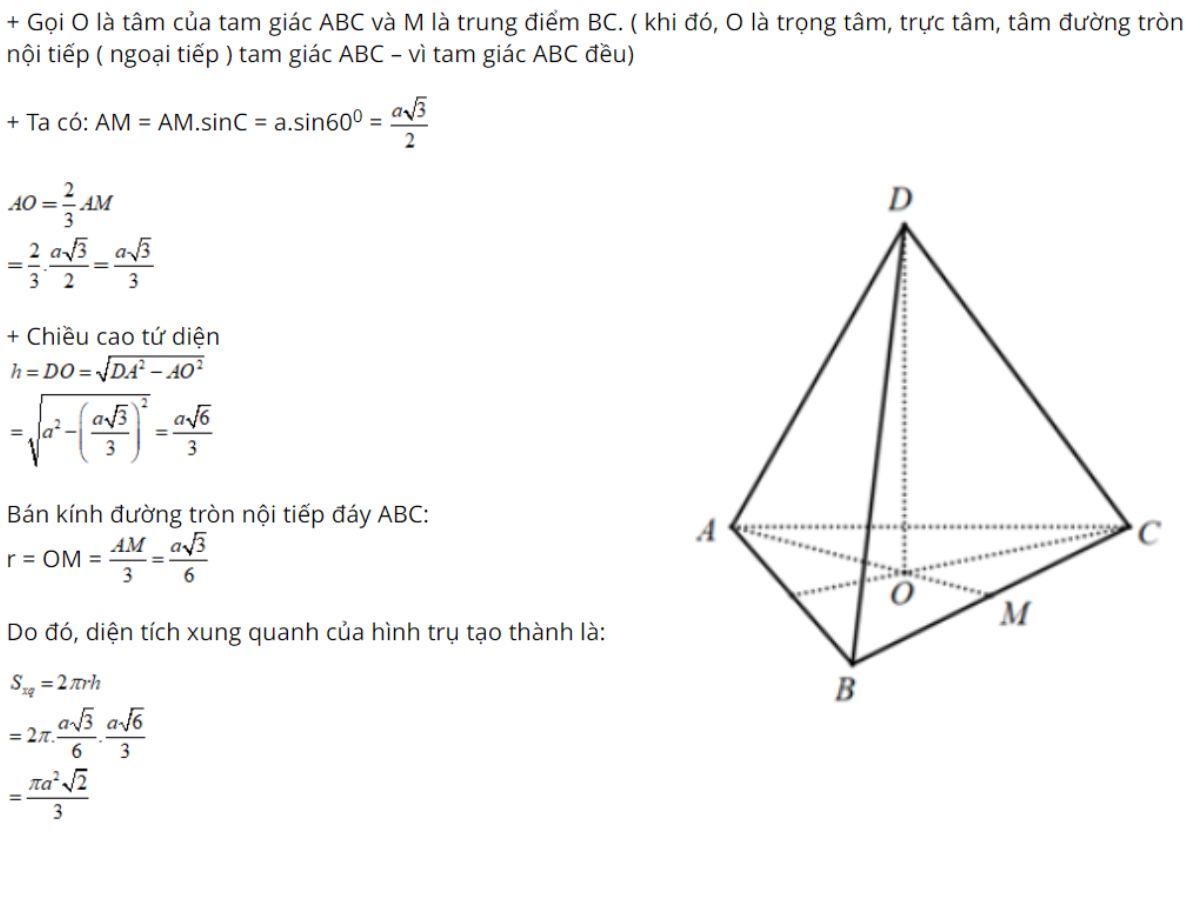
Một số kiến thức các em có thể quan tâm:
Hình nón là gì? Công thức tính diện tích và thể tích
Hình cầu là gì? Công thức tính diện tích và thể tích
Chúc mừng các em, vậy là chúng ta đã cùng nhau làm xong chuỗi bài tập hình trụ rồi. Các em truy cập hoctot.hocmai.vn để tìm hiểu thêm những kiến thức bổ ích và những bài tập ôn luyện nhé. HOCMAI luôn mong muốn đem lại những bài học bổ ích cho các em để các em vượt qua mọi thử thách khi tới trường.


















