Cung chứa góc là một trong những chuyên đề nổi bật trong chương trình hình học toán 9. Đây là chuyên đề quan trọng và có nhiều mối liên hệ với các chuyên đề toán học khác. Vậy các em học sinh đã biết cung chứa góc là gì chưa? Cách giải bài tập cho từng dạng như thế nào? Hãy cùng HOCMAI tìm hiểu chi tiết qua bài viết này nhé.
Bài viết tham khảo thêm:
I. Tóm tắt lý thuyết cần nắm về Cung chứa góc
1. Quỹ tích cung chứa góc
Với đoạn thẳng AB cho trước và góc α (0° < α < 180°) cho trước thì quỹ tích (tập hợp) các điểm M thỏa mãn điều kiện góc AMB = α là hai cung chứa góc α dựng trên đoạn thẳng AB.
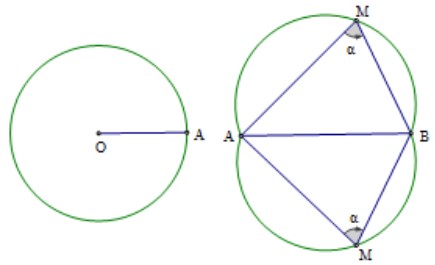
Chú ý:
– Hai cung chứa góc α nói trên là hai cung tròn đối xứng nhau qua đoạn thẳng AB. Hai điểm A, B được xem là thuộc quỹ tích.
– Quỹ tích (tập hợp) các điểm M nhìn đoạn thẳng AB cho trước dưới một góc vuông là đường tròn có đường kính AB
2. Cách vẽ cung chứa góc a
Bài toán: Cho đoạn thẳng AB và góc α (0° < α < 180°). Tìm tập hợp (quỹ tích) các điểm M sao cho góc AMB = α.
Để tìm được tập hợp các điểm M thỏa mãn điều kiện cho trước: góc AMB = α, ta cần thực hiện theo các bước sau:
– Vẽ đường trung trực của đoạn thẳng AB là d;
– Vẽ tia Ax tạo với đoạn thẳng AB một góc α;
– Vẽ đường thẳng Ay vuông góc với tia Ax. Gọi giao điểm của đường thẳng Ay với d là O.
– Vẽ cung AmB của đường tròn tâm O và bán kính OA sao cho cung này nằm tại nửa mặt phẳng bờ AB và không chứa tia Ax.
Cung AmB được vẽ như các bước trên là một cung chứa góc α.
3. Cách giải bài toán quỹ tích
Muốn chứng minh quỹ tích hoặc tập hợp các điểm M thoả mãn tính chất T là một hình H nào đó, ta cần phải chứng minh hai phần:
- Phần thuận: Mọi điểm có tính chất T sẽ đều thuộc hình H.
- Phần đảo: Mọi điểm thuộc hình H sẽ đều có tính chất T.
Từ đó ta đi đến kết luận rằng quỹ tích các điểm M có tính chất T là hình H.
(Thông thường khi gặp bài toán: “Tìm quỹ tích …” thì ta nên dự đoán hình H trước khi bắt đầu chứng minh).
II. Các dạng toán thường gặp về cung chứa góc
Dạng 1. Quỹ tích là cung chứa góc
Phương pháp giải: Để làm dạng toán này, chúng ta cần thực hiện theo ba bước sau:
- Bước 1: Tìm đoạn thẳng cố định có trong hình vẽ;
- Bước 2: Nối điểm cần tìm với hai đầu của đoạn thẳng cố định đó, xác định góc a không đổi;
- Bước 3: Khẳng định quỹ tích điểm cần tìm là cung chứa góc a dựng trên một đoạn thẳng cố định.
Ví dụ 1: Cho tam giác ABC có đoạn thẳng BC cố định và số đo góc A bằng 50°. Gọi giao điểm của ba đường phân giác trong tam giác là D. Tìm quỹ tích điểm D.
Lời giải:
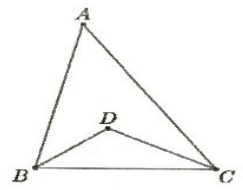
Ta có:
Góc A = 50° => Góc B + góc C = 180° – 50° = 130°
=> Góc DBC + DCB = 65° => Góc BDC = 115°
Vậy quỹ tích của điểm D là hai cung chứa góc 115° dựng trên đoạn BC.
Ví dụ 2: Cho tam giác ABC (vuông tại A) có cạnh BC cố định. Gọi giao điểm của ba đường phân giác trong tam giác là I. Tìm quỹ tích điểm I khi thay đổi điểm A.
Lời giải:
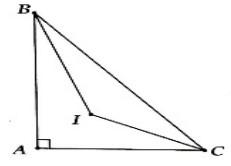
Ta có:
Góc A = 90° => Góc B + góc C = 180° – 90° = 90°
=> Góc IBC + ICB = 45° => Góc BDC = 135°
Vậy quỹ tích của điểm I là hai cung có chứa góc 135° dựng trên đoạn BC.
Dạng 2. Chứng minh nhiều điểm cùng thuộc đường tròn
Phương pháp giải: Để làm được dạng toán này, chúng ta cần chứng minh nhiều điểm cùng thuộc một nửa mặt phẳng bờ là AB và cùng nhìn đoạn AB cố định dưới một góc không đổi.
Ví dụ 1: Cho một nửa đường tròn có đường kính AB. Gọi điểm chính giữa của cung AB là M. Trên cung AM lấy điểm N. Trên tia đối của MA lấy D sao cho MD = MB, trên tia đối của NB lấy E sao cho NA = NE, trên tia đối của MB lấy C sao cho MC = MA. Chứng minh rằng 5 điểm A, B, C, D và E cùng nằm trên (thuộc) một đường tròn.
Lời giải:
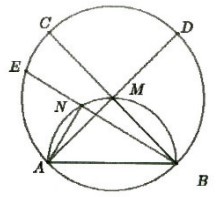
Các tam giác ΔANE, ΔAMC, ΔBMD vuông cân
=> Góc AEB = Góc ADB = Góc ACB = 45°
Mà AB cố định nên các điểm A, B, C, D và E cùng nằm trên (thuộc) một đường tròn
Ví dụ 2: Cho I, O lần lượt là tâm đường tròn nội tiếp, ngoại tiếp của tam giác ABC với A = 60°. Gọi H là trực tâm của ΔABC. Chứng minh rằng các điểm B, C, O, H và I cùng thuộc một đường tròn.
Lời giải:
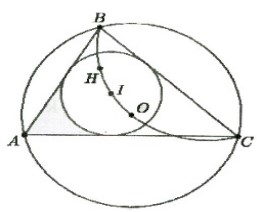
Dễ dàng chứng minh được góc BIC = 120°
=> Góc BOC = 2 lần góc BAC = 120°
=> Góc BHC = 180° – 60° = 120°(Góc nội tiếp và góc ở tâm)
Mà BC cố định nên các điểm B, C, O, H, I cùng thuộc một đường tròn
Dạng 3. Dạng cung chứa góc
Phương pháp giải: Để hoàn thành dạng toán này, chúng ta cần thực hiện lần lượt 4 bước sau:
- Bước 1: Vẽ đường trung trực của đoạn thẳng AB là d;
- Bước 2: Vẽ tia Ax tạo với đường thẳng AB một góc;
- Bước 3: Vẽ đường thẳng Ay vuông góc với tia Ax. Gọi giao điểm của Ay với d là O.
- Bước 4: Vẽ cung AmB, tâm Om với bán kính là OA sao cho cung này nằm tại nửa mặt phẳng bờ AB và không chứa tia Ax.
Cung AmB được vẽ như các bước trên là một cung chứa góc α.
Ví dụ: Dựng một cung chứa góc 55° trên đoạn thẳng AB = 3cm.
Lời giải:
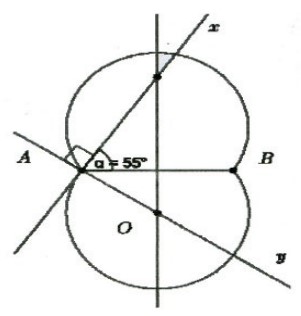
Các bước cần thực hiện:
- Bước 1: Vẽ đoạn thẳng AB có độ dài bằng 3cm, dựng trung trực d của đoạn thẳng AB;
- Bước 2: Vẽ tia Ax tạo với AB một góc = 55°;
- Bước 3: Vẽ Ay ⊥ Ax cắt d ở O;
- Bước 4: Vẽ cung AmB tâm O, bán kính OA sao cho cung này nằm trên nửa mặt phẳng bờ AB không chứa tia Ax.
Cung AmB như trên là cung cần vẽ.
Bài tập trắc nghiệm
Câu 1: Cho tam giác ABC, BC cố định và số đo góc A bằng 50°. Gọi giao điểm của ba đường phân giác trong của tam giác là D. Tìm quỹ tích điểm D.
A. Một cung chứa góc 115° dựng trên đoạn BC.
B. Một cung chứa góc 115° dựng trên đoạn AC.
C. Hai cung chứa góc 115° dựng trên đoạn AB.
D. Hai cung chứa góc 115° dựng trên đoạn BC.
Lời giải:
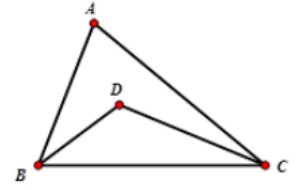
Ta có: Góc A = 50° => Góc B + Góc C = 130°
=> Góc BDC + Góc DCB = 65°
=> Góc BDC = 115°
Vậy quỹ tích của điểm D là hai cung chứa góc 115° dựng trên đoạn BC.
Vậy D là đáp án chính xác
Câu 2: Cho các hình thoi ABCD có cạnh AB cố định. Tìm quỹ tích giao điểm O của hai đường thẳng chéo nhau ở hình thoi đó.
A. Quỹ tích điểm O là 2 cung chứa góc 120° dựng trên AB.
B. Quỹ tích điểm O là một nửa đường tròn có đường kính AB , trừ hai điểm A và B.
C. Quỹ tích điểm O là 2 cung chứa góc 60° dựng trên AB.
D. Quỹ tích điểm O là 2 cung chứa góc 30° dựng trên AB.
Lời giải:
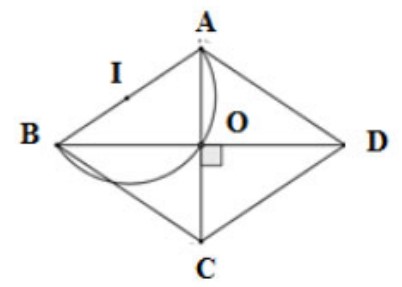
Xét hình thoi ABCD có hai đường chéo là AC và BD vuông góc với nhau ở trung điểm của mỗi đường.
=> AO ⊥ BO => Góc AOB = 90°
Ta có góc AOB = 90° không đổi mà A, B, cố định.
=> Quỹ tích điểm O là nửa đường tròn có đường kính AB trừ hai điểm A và B .
Vậy B là đáp án chính xác
Câu 3: Cho một nửa đường tròn có đường kính AB. Gọi điểm chính giữa của cung ABM là M. Trên cung AM lấy điểm N. Trên tia đối của tia MA lấy điểm D sao cho MD = MB , trên tia đối của NB lấy E sao cho NA = NE, trên tia đối của MB lấy C sao cho MC = MA. Các điểm nào dưới đây nằm trên (thuộc) một đường tròn?
A. A, B, C, M, E.
B. M, B, C, D, N.
C. A, B, C, D, E.
D. A, B, C, D, N.
Lời giải:
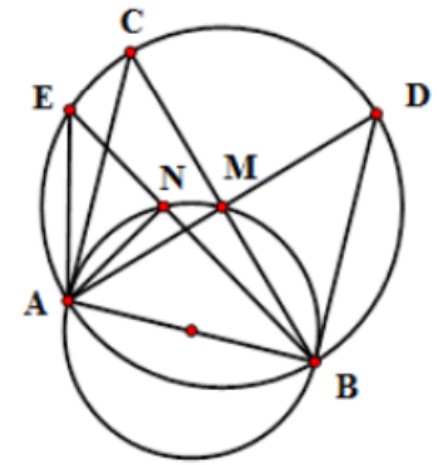
Các tam giác ΔANE, ΔAMC, ΔBMD lần lượt vuông cân tại 3 điểm N, M, M.
=> Góc AEB = Góc ADB = Góc ACB = 45°
Mà AB cố định nên bốn điểm A, B, C, D và E cùng nằm trên một đường tròn.
Vậy C là đáp án chính xác
Câu 4: Cho tam giác ABC đều. Tìm quỹ tích các điểm M nằm trong tam giác đó thỏa mãn:
MA² = MB² + MC².
A. Quỹ tích điểm M là hai cung chứa góc 150° dựng trên BC, trừ hai điểm B và C.
B. Quỹ tích điểm M là đường tròn có đường kính là BC.
C. Quỹ tích điểm M là đường tròn có đường kính là BC trừ hai điểm B và C.
D. Quỹ tích điểm M là 2 cung chứa góc 150° dựng trên BC.
Lời giải:
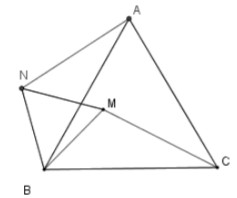
Vẽ ΔBMN đều (Trong đó N khác phía CC đối với BM).
Xét hai tam giác ΔBNA và ΔBMC có:
- BN = BM (Vì tam giác BMN đều)
- BA = BC (Vì tam giác ABC đều)
- Góc NBA = Góc MBC (Vì cùng bằng 60° – góc ABM)
=> ΔBNA = ΔBMC (góc – cạnh – góc) => NA = MC
Ta có: MA² = MB² + MC² = MN² +NA² nên góc MNA = 90°
=> Góc BNA = 90° + 60° = 150° => Góc BMC = Góc BNA = 150°
Mà B, C cố định => Quỹ tích điểm M là hai cung chứa góc 150° dựng trên BC, trừ hai điểm B và C.
Vậy A là đáp án chính xác
(Hết)
Trên đây là tóm tắt lý thuyết, các dạng và cách giải chi tiết các bài tập liên quan tới Cung chứa góc. Tuy chuyên đề này không khó nhưng đòi hỏi bạn cần có sự tập trung để không gặp phải khó khăn khi dựng hình và chứng minh. Nếu có câu hỏi, thắc mắc nào về nội dung bài viết, hãy để lại bình luận ngay dưới bài viết của HOCMAI nhé!





















