Đề cương ôn thi học kì 1 Toán 6 theo chương trình mới được HOCMAI biên soạn đầy đủ theo ba bộ sách mới là Cánh Diều, Kết nối tri thức và Chân trời sáng tạo. Các em học sinh hãy tham khảo thật kỹ để chuẩn bị tốt nhất cho kỳ thi cuối HK1 sắp tới nhé!
Tham khảo thêm:
- Đề cương ôn thi học kì 1 ngữ văn 6 sách Cánh diều
- Đề cương ôn thi học kì 1 ngữ văn 6 sách Kết nối tri thức
- Đề cương ôn thi học kì 1 ngữ văn 6 sách Chân trời sáng tạo
- Đề cương ôn thi HK1 1 Khoa Học Tự Nhiên lớp 6 Chân trời sáng tạo
- Đề cương ôn thi HK1 1 Khoa Học Tự Nhiên lớp 6 Kết nối tri thức
- Đề cương ôn thi HK1 1 Khoa Học Tự Nhiên lớp 6 Cánh Diều
I – Đề cương ôn thi học kì 1 Toán 6 theo chương trình mới | Đại số
Chương I – Tập hợp các số tự nhiên
A – Tập hợp
1. Khái niệm tập hợp và phần tử của tập hợp
Một tập hợp (gọi tắt là tập) bao gồm những đối tượng nhất định. Chúng được gọi là những phần tử của tập hợp đó.
- x là một phần tử của tập A, kí hiệu là x ∈ A (đọc là x thuộc A)
- y không là phần tử của tập A, kí hiệu là y ∉ A (đọc là y không thuộc A)
Chú ý. Khi x thuộc A, ta còn nói “x nằm trong A”, hay “A chứa x”.
2. Các kí hiệu
– Người ta thường dùng các chữ in hoa A,B,C,.. để kí hiệu tập hợp, các chữ in thường a,b,c,…để kí hiệu phần tử của tập hợp.
– Các phần tử của một tập hợp được viết trong hai dấu ngoặc nhọn { }, cách nhau bởi dấu phẩy “,” hoặc dấu chấm phẩy “;” (đối với trường hợp các phần tử là số).
– Mỗi phần tử được liệt kê một lần, thứ tự liệt kê tùy ý.
– Phần tử x thuộc tập hợp A được kí hiệu là x ∈ A, đọc là “x thuộc A”.
Phần tử y không thuộc tập hợp A được kí hiệu là y ∉ A, đọc là “y không thuộc A”.
– Tập hợp không chứa phần tử nào gọi là tập rỗng, kí hiệu là ∅
Chú ý. Ta viết n ∈ N có nghĩa n là một số tự nhiên.
3. Mô tả một tập hợp
Để cho một tập hợp, thường có hai cách:
a) Liệt kê các phần tử của tập hợp.
b) Chỉ ra tính chất đặc trưng cho các phần tử của tập hợp.
Ngoài hai cách trên, người ta còn minh họa tập hợp bằng một vòng kín, mỗi phần tử của tập hợp được biểu diễn bởi một dấu chấm bên trong vòng kín đó. Ta nói tập hợp được minh họa bằng sơ đồ Venn.
B – Cách ghi số tự nhiên
1. Hệ thập phân
Số tự nhiên được viết trong hệ thập phân bởi một, hai hay nhiều chữ số. Các chữ số được dùng là 0;1;2;3;4;5;6;7;8;9. Khi một số gồm hai chữ số trở lên thì chữ số đầu tiên (tính từ trái sang phải) khác 0.
Khi viết các số tự nhiên có từ 4 chữ số trở lên, ta nên viết tách riêng từng nhóm ba chữ số kể từ phải sang trái cho dễ đọc.
Trong cách viết một số tự nhiên có nhiều chữ số, mỗi chữ số ở những vị trí khác nhau có giá trị khác nhau.
– Kí hiệu ab chỉ số tự nhiên có hai chữ số, chữ số hàng chục là a (a ≠ 0), chữ số hàng đơn vị là b.
Ta có: ab = ax10 + b.
– Kí hiệu abc chỉ số tự nhiên có ba chữ số, chữ số hàng trăm là a (a ≠ 0), chữ số hàng chục là b, chữ số hàng đơn vị là c. Ta có:
abc = ax100 + bx10 + c.
– Với các số cụ thể thì không viết dấu gạch ngang ở trên.
2. Số La Mã
Ngoài cách ghi số trong hệ thập phân gồm các chữ số từ 0 đến 9 và các hàng (đơn vị, chục, trăm, nghìn, …) như trên, còn có cách ghi số La Mã như sau:
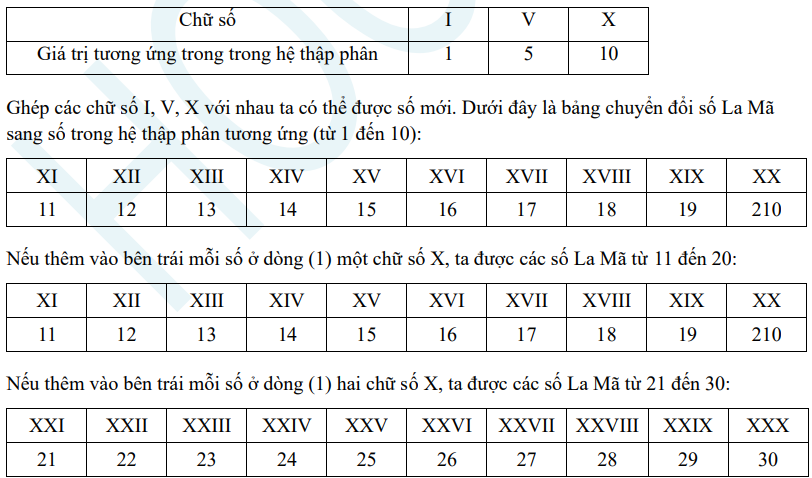
Ta có thể gặp chữ số La Mã trên mặt đồng hồ, đánh số chương mục của sách, đánh số thế kỉ,… Mỗi chữ số La Mã có giá trị không phụ thuộc vào vị trí của nó trong số La Mã. Hệ La Mã không có số 0.
C – Thứ tự trong tập hợp các số tự nhiên C
1. Thứ tự trong tập hợp số tự nhiên
Các số tự nhiên được biểu diễn trên tia số. Mỗi số tự nhiên ứng với một điểm trên tia số, điểm biểu diễn cho số tự nhiên n gọi là điểm n.
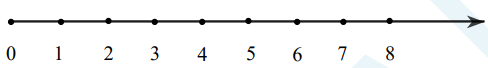
Trong hai số tự nhiên a và b khác nhau, có một số nhỏ hơn số kia. Nếu số a nhỏ hơn số b ta viết a <b (a nhỏ hơn b). Ta cũng nói số b lớn hơn số a và viết b > a.
Khi biểu diễn trên tia số nằm ngang có chiều mũi tên đi từ trái sang phải, nếu a < b thì điểm a nằm bên trái điểm b.
Ta viết a ≤ b để chỉ a < b hoặc a = b, để chỉ b > a hoặc b = a.
Mỗi số tự nhiên có một số liền sau cách nó một đơn vị. Hai số đó được gọi là hai số tự nhiên liên tiếp.
Tính chất bắc cầu: Nếu a < b và b < c thì a < c .
Với số tự nhiên a cho trước:
– Ta viết x ≤ a để chỉ x < a hoặc x = a.
– Ta viết x ≥ a để chỉ x > a hoặc x = a.
2. So sánh hai số tự nhiên
– Trong hai số tự nhiên có số chữ số khác nhau: Số nào có nhiều chữ số hơn thì lớn hơn, số nào có ít chữ số hơn thì nhỏ hơn.
– Để so sánh hai số tự nhiên có số chữ số bằng nhau, ta lần lượt so sánh từng cặp chữ số trên cùng một hàng (tính từ trái sang phải), cho đến khi xuất hiện cặp chữ số đầu tiên khác nhau. Ở cặp chữ số khác nhau đó, chữ số nào lớn hơn thì số tự nhiên chứa chữ số đó lớn hơn.
D – Phép cộng và phép trừ số tự nhiên
1. Phép cộng
Phép cộng các số tự nhiên: a+b = c
Trong đó: a và b là các số hạng, c là tổng
Phép cộng các số tự nhiên có tính chất giao hoán, kết hợp, cộng với số 0.
Cụ thể:
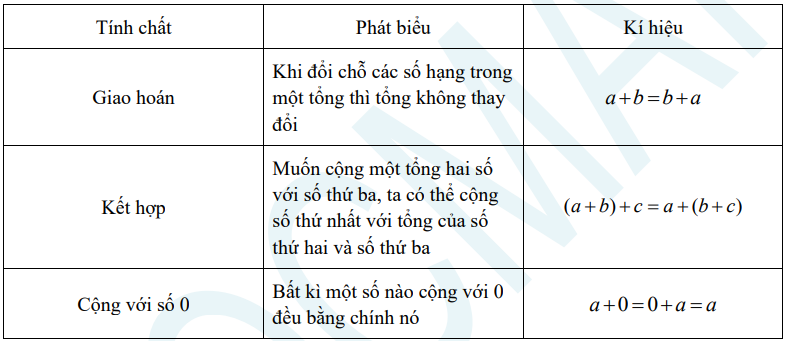
Do tính chất kết hợp nên giá trị của biểu thức a+b+c có thể được tính theo một trong hai cách sau: a+b+c = (a+b) + c hoặc a+b+c = a+ (b + c).
2. Phép trừ
Phép trừ một số tự nhiên cho một số tự nhiên nhỏ hơn hoặc bằng nó: a-b = c (a ≥ b). Trong đó: a là số bị trừ, b là số trừ, c là hiệu.
Nếu a−b = c thì a = b+c.
Nếu a + b = c thì a = c – b và b = c – a.
E – Thứ tự trong tập hợp các số tự nhiên
1. Phép nhân
Phép nhân các số tự nhiên: a x b = c , trong đó a, b là các thừa số, c là tích.
Quy ước:
– Trong một tích, ta có thể thay dấu nhân “x” bằng dấu chấm “.”.
– Trong một tích mà các thừa số đều bằng chữ hoặc chỉ có một thừa số bằng số, ta có thể không cần viết dấu nhân giữa các thừa số.
a) Nhân hai số có nhiều chữ số
Sau khi đặt tính ta thực hiện theo các bước sau:
– Tính tích riêng thứ nhất: Ta lấy chữ số hàng đơn vị của số phía bên dưới nhân với số bên trên lần lượt theo thứ tự từ phải sang trái.
– Tính tích riêng thứ hai: Lấy chữ số hàng chục của số bên dưới nhân với số bên trên theo thứ tự từ phải sang trái. Tích này viết lùi sang bên trái một cột so với tích riêng thứ nhất.
– Tính tích riêng thứ ba: Lấy chữ số hàng trăm của số bên dưới nhân với số bên trên theo thứ tự từ phải sang trái. Tích này viết lùi sang bên trái hai cột so với tích riêng thứ nhất.
– Cộng các tích riêng theo cột dọc, ta được tích hai số có nhiều chữ số cần tìm.
b) Tính chất của phép nhân

2. Phép chia

F – Lũy thừa với số mũ tự nhiên
Đối với tích của nhiều thừa số bằng nhau ta có thể viết gọn thành một lũy thừa.
Phép nhân nhiều thừa số bằng nhau gọi là phép nâng lên lũy thừa.

G – Thứ tự thực hiện các phép tính
1. Thứ tự thực hiện các phép tính trong biểu thức không chứa dấu ngoặc
– Khi biểu thức chỉ có các phép tính cộng và trừ (hoặc chỉ có các phép tính nhân và chia), ta thực hiện phép tính theo thứ tự từ trái sang phải.
– Khi biểu thức có các phép tính cộng, trừ, nhân, chia, ta thực hiện phép tính nhân và chia trước, rồi đến cộng và trừ.
– Khi biểu thức có các phép tính cộng, trừ, nhân, chia, nâng lên lũy thừa, ta thực hiện phép tính nâng lên lũy thừa trước, rồi đến nhân và chia, cuối cùng đến cộng và trừ.
2. Thứ tự thực hiện các phép tính trong biểu thức chứa dấu ngoặc
– Khi biểu thức có chứa dấu ngoặc, ta thực hiện các phép tính trong dấu ngoặc trước.
– Nếu biểu thức có các dấu ngoặc tròn ( ), ngoặc vuông [ ], ngoặc nhọn { }, ta thực hiện phép tính trong dấu ngoặc tròn trước, rồi thực hiện phép tính trong dấu ngoặc vuông, cuối cùng thực hiện phép tính trong dấu ngoặc nhọn:
( ) → [ ] → { }
Chương II – Tính chia hết trong tập hợp số tự nhiên
A – Quan hệ chia hết và tính chất
1. Quan hệ chia hết
a) Khái niệm về chia hết
Cho hai số tự nhiên a và b (b ≠ 0).
Nếu có số tự nhiên q sao cho a = b.q thì ta nói a chia hết cho b.
Khi a chia hết cho b, ta nói a là bội của b và b là ước của a.
– Nếu số dư trong phép chia a cho b bằng 0 thì a chia hết cho b.
– Nếu số dư trong phép chia a cho b khác 0 thì a không chia hết cho b.
Với a là số tự nhiên khác 0 thì:
– a là ước của a;
– a là bội của a;
– 0 là bội của a;
– 1 là ước của a.
b) Cách tìm bội và ước của một số
Để tìm các bội của n (n ∈ N*), ta có thể lần lượt nhân n với 0, 1, 2, 3,…. Khi đó các kết quả nhận được đều là bội của n.
Để tìm ra các ước của số tự nhiên n lớn hơn 1, ta có thể lần lượt chia n cho các số tự nhiên từ 1 đến n. Khi đó các phép chia hết cho ta số chia là ước của n.
Ta kí hiệu Ư(a) là tập hợp các ước của a và B(b) là tập hợp các bội của b.
2. Tính chất chia hết của một tổng
Nếu tất cả các số hạng của tổng đều chia hết cho cùng một số thì tổng chia hết cho số đó.

3. Tính không chia hết
Nếu có một số hạng của một tổng không chia hết cho một số đã cho, các số hạng còn lại đều chia hết cho số đó thì tổng không chia hết cho số đã cho.
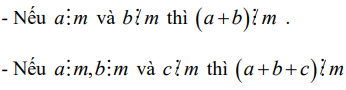
B – Dấu hiệu chia hết
1. Dấu hiệu chia hết cho 2
Các số có chữ số tận cùng là 0, 2, 4, 6, 8 (tức là số chẵn) thì chia hết cho 2 và chỉ những số đó mới chia hết cho 2.
2. Dấu hiệu chia hết cho 5
Các số có chữ số tận cùng là 0 hoặc 5 thì chia hết cho 5 và chỉ những số đó mới chia hết cho 5.
3. Dấu hiệu chia hết cho 3
Các số có tổng các chữ số chia hết cho 3 thì chia hết cho 3 và chỉ những số đó mới chia hết cho 3.
4. Dấu hiệu chia hết cho 9
Các số có tổng các chữ số chia hết cho 9 thì chia hết cho 9 và chỉ những số đó mới chia hết cho 9.
C – Số nguyên tố
1. Số nguyên tố. Hợp số
Số nguyên tố là số tự nhiên lớn hơn 1, chỉ có hai ước là 1 và chính nó.
Hợp số là số tự nhiên lớn hơn 1, có nhiều hơn hai ước.
– Số 0 và số 1 không là số nguyên tố cũng không là hợp số.
– Để chứng tỏ số tự nhiên a lớn hơn 1 là một hợp số, ta chỉ cần tìm một ước của a khác 1 và khác a.
– Nếu số nguyên tố p là ước của số tự nhiên a thì p được gọi là ước nguyên tố của a.
2. Cách tìm một ước nguyên tố của một số
Để tìm một ước nguyên tố của số a ta có thể làm như sau: Lần lượt thực hiện phép chia a cho các số nguyên tố theo thứ tự tăng dần 2, 3, 5, 7, 11, 13, …
Khi đó phép chia hết đầu tiên cho ta số chia là một ước nguyên tố của a.
3. Phân tích một số ra thừa số nguyên tố
Phân tích một số tự nhiên lớn hơn 1 ra thừa số nguyên tố là viết số đó dưới dạng một tích các thừa số nguyên tố.
Ta nên chia mỗi số cho ước nguyên tố nhỏ nhất của nó.
Cứ tiếp tục chia như thế cho đến khi được thương là 1.
Có hai phương pháp phân tích một số ra thừa số nguyên tố: Phương pháp phân tích theo sơ đồ cây và phương pháp phân tích theo sơ đồ cột.
Chú ý:
– Mọi số tự nhiên lớn hơn 1 đều phân tích được thành tích các thừa số nguyên tố.
– Mỗi số nguyên tố chỉ có một dạng phân tích ra thừa số nguyên tố là chính số đó.
– Có thể viết gọn dạng phân tích một số ra thừa số nguyên tố bằng cách dùng lũy thừa.
– Thông thường, khi phân tích một số tự nhiên ra thừa số nguyên tố, các ước nguyên tố được viết theo thứ tự tăng dần.
– Người ta quy ước dạng phân tích ra thừa số nguyên tố của một số nguyên tố là chính nó.
– Ngoài cách làm như trên, ta cũng có thể phân tích một số ra thừa số nguyên tố bằng cách viết số đó thành tích của hai thừa số một cách linh hoạt.
Nhận xét:
Dù phân tích một số ra thừa số nguyên tố bằng cách nào thì cuối cùng ta cũng được cùng một kết quả.
D – Ước chung. Ước chung lớn nhất
1. Ước chung và ước chung lớn nhất
Số tự nhiên n được gọi là ước chung của hai số a và b nếu n vừa là ước của a vừa là ước của b.
Số lớn nhất trong các ước chung của a và b được gọi là ước chung lớn nhất của a và b.
Quy ước: Viết tắt ước chung là ƯC và ước chung lớn nhất là ƯCLN.

Chú ý: Số tự nhiên n được gọi là ước chung của ba số a, b, c nếu n là ước của cả ba số a, b, c.
Ước chung của hai số là ước của ước chung lớn nhất của chúng.
Để tìm ước chung của các số, ta có thể làm như sau:
– Tìm ƯCLN của các số đó.
– Tìm các ước của ƯCLN đó.
2. Tìm ước chung lớn nhất bằng cách phân tích ra thừa số nguyên tố
Tìm ước chung lớn nhất bằng cách phân tích các số ra thừa số nguyên tố
Bước 1. Phân tích mỗi số ra thừa số nguyên tố.
Bước 2. Chọn ra các thừa số nguyên tố chung, mỗi thừa số lấy với số mũ nhỏ nhất.
Bước 3. Lấy tích của các lũy thừa đã chọn, ta nhận được ước chung lớn nhất cần tìm.
Chú ý:
– Nếu hai số đã cho không có thừa số nguyên tố chung thì ƯCLN của chúng bằng 1.
– Nếu a chia hết cho b thì ƯCLN (a, b) = b.
3. Rút gọn về phân số tối giản

E – Bội chung. bội chung nhỏ nhất
1. Bội chung và bội chung nhỏ nhất
Số tự nhiên n được gọi là bội chung của hai số a và b nếu n vừa là bội của a vừa là bội của b.

Bội chung của nhiều số là bội của bội chung nhỏ nhất của chúng.
Để tìm bội chung của nhiều số, ta có thể lấy bội chung nhỏ nhất của chúng lần lượt nhân với 0,1,2,..
2. Tìm bội chung nhỏ nhất bằng cách phân tích các số ra thừa số nguyên tố
Tìm bội chung nhỏ nhất bằng cách phân tích các số ra thừa số nguyên tố:
Bước 1. Phân tích mỗi số ra thừa số nguyên tố.
Bước 2. Chọn ra các thừa số nguyên tố chung và các thừa số nguyên tố riêng, mỗi thừa số lấy với số mũ lớn nhất.
Bước 3. Lấy tích của các lũy thừa đã chọn, ta nhận được bội chung nhỏ nhất cần tìm.
3. Tìm bội chung từ bội chung nhỏ nhất
Để tìm bội chung của các số đã cho ta có thể làm như sau:
Bước 1. Tìm BCNN của các số.
Bước 2. Tìm các bội của BCNN đó.
4. Ứng dụng của bội chung nhỏ nhất

Chương III – Số nguyên
A – Tập hợp các số nguyên
1. Làm quen với số nguyên âm
Các số -1, -2, -3, … là các số nguyên âm. Số nguyên âm được nhận biết bằng dấu “-“ ở trước số tự nhiên khác 0.
Số nguyên âm được sử dụng trong nhiều tình huống thực tiễn cuộc sống:
– Số nguyên âm được dùng để chỉ nhiệt độ dưới 0°C .
– Số nguyên âm được dùng để chỉ độ cao dưới mực nước biển.
– Số nguyên âm được dùng để chỉ số tiền nợ, cũng như để chỉ số tiền lỗ trong kinh doanh.
– Số nguyên âm được dùng để chỉ thời gian trước công nguyên.
2. Tập hợp Z các số nguyên
– Số tự nhiên khác 0 còn được gọi là số nguyên dương.
– Các số nguyên âm, số 0 và các số nguyên dương tạo thành tập hợp các số nguyên.
– Tập hợp các số nguyên được kí hiệu là Z.
Chú ý:
– Số 0 không phải số nguyên âm, cũng không phải số nguyên dương.
– Các số nguyên dương 1, 2, 3, … đều mang dấu “+” nên còn được viết là +1, +2, +3, …
3. Biểu diễn số nguyên trên trục số
Ta có thể biểu diễn số nguyên trên trục số. Điểm biểu diễn số nguyên a gọi là điểm a.
Có hai loại trục số như sau:
a) Trục số nằm ngang có:
– Chiều dương hướng từ trái sang phải (được đánh dấu bằng mũi tên)
– Điểm gốc của trục số là điểm 0 (biểu diễn số 0)
– Đơn vị đo độ dài trên trục số là độ dài đoạn thẳng nối điểm 0 với điểm 1 (biểu diễn số 1 và nằm bên phải điểm 0)
![]()
b) Trục số thẳng đứng:
– Chiều dương hướng từ dưới lên trên (được đánh dấu bằng mũi tên)
– Điểm gốc của trục số là điểm 0 (biểu diễn số 0)
– Đơn vị đo độ dài trên trục số là độ dài đoạn thẳng nối điểm 0 với điểm 1 (biểu diễn số 1 và nằm phía trên điểm 0)
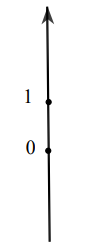
Trên trục số nằm ngang, điểm biểu diễn số nguyên âm nằm bên trái điểm 0, điểm biểu diễn số nguyên dương nằm bên phải điểm 0.
Trên trục số thẳng đứng, điểm biểu diễn số nguyên âm nằm phía dưới điểm 0, điểm biểu diễn số nguyên dương nằm phía trên điểm 0.
Chú ý. Khi nói “trục số” mà không nói gì thêm, ta hiểu là nói về trục số nằm ngang.
5. So sánh hai số nguyên
– So sánh hai số nguyên khác dấu: Số nguyên âm luôn nhỏ hơn số nguyên dương.
– So sánh hai số nguyên cùng dấu:
Để so sánh hai số nguyên âm, ta làm như sau:
Bước 1. Bỏ dấu “-“ trước cả hai số âm
Bước 2. Trong hai số nguyên dương nhận được, số nào nhỏ hơn thì số nguyên âm ban đầu (tương ứng) sẽ lớn hơn.
B – Phép cộng và phép trừ số nguyên
1. Phép cộng hai số nguyên cùng dấu
a) Cộng hai số nguyên dương
Muốn cộng hai số nguyên dương, ta cộng chúng như cộng hai số tự nhiên.
b) Cộng hai số nguyên âm
Muốn cộng hai số nguyên âm, ta cộng phần số tự nhiên của chúng với nhau rồi thêm dấu trừ đằng trước kết quả.
Tổng của hai số nguyên cùng dấu luôn cùng dấu với hai số nguyên đó:
– Tổng của hai số nguyên dương là số nguyên dương.
– Tổng của hai số nguyên âm là số nguyên âm.
2. Phép cộng hai số nguyên khác dấu
Để cộng hai số nguyên khác dấu, ta làm như sau:
– Nếu số dương lớn hơn số đối của số âm thì ta lấy số dương trừ đi số đối của số âm.
– Nếu số dương bé hơn số đối của số âm thì ta lấy số đối của số âm trừ đi số dương rồi thêm dấu trừ trước kết quả.
Chú ý:
– Hai số nguyên đối nhau luôn có tổng bằng 0.
– Số đối của 0 là chính nó.
Khi cộng hai số nguyên trái dấu:
– Nếu số dương lớn hơn số đối của số âm thì ta có tổng dương.
– Nếu số dương bằng số đối của số âm thì ta có tổng bằng 0.
– Nếu số dương bé hơn số đối của số âm thì ta có tổng âm.
3. Tính chất của phép cộng các số nguyên
Phép cộng các số nguyên có các tính chất sau:
– Giao hoán: a+b = b+a
– Kết hợp: (a+b) + c = a + (b+c)
4. Phép trừ số nguyên
– Muốn trừ số nguyên a cho số nguyên b, ta cộng a với số đối của b: a – b = a + (-b)
C – Quy tắc dấu ngoặc
Quy tắc dấu ngoặc:
– Khi bỏ dấu ngoặc có dấu “+” đằng trước thì giữ nguyên dấu của các số hạng trong ngoặc.
- a + (b+c) = a+b+c
- a + (b-c) = a+b-c
– Khi bỏ dấu ngoặc có dấu “-“ đằng trước, ta phải đổi dấu của các số hạng trong ngoặc: dấu “+” thành dấu “-“ và dấu “-“ thành dấu “+”.
- a – (b+c) = a-b-c
- a – (b-c) = a-b+c
D – Phép nhân số nguyên
1. Phép nhân hai số nguyên khác dấu
Muốn nhân hai số nguyên khác dấu, ta nhân phần số tự nhiên của hai số đó với nhau rồi đặt dấu “-“ trước kết quả nhận được.
Nếu m, n ∈ N* → m.(-n) = (-n).m = -(m.n).
Tích của hai số nguyên khác dấu luôn là số nguyên âm.
2. Phép nhân hai số nguyên cùng dấu
a) Phép nhân hai số nguyên dương
Nhân hai số nguyên dương chính là nhân hai số tự nhiên khác 0.
b) Phép nhân hai số nguyên âm
Muốn nhân hai số nguyên âm, ta nhân phần số tự nhiên của hai số đó với nhau.
Nếu m, n ∈ N* → (-m).(-n) = (-n).(-m) = m.n.
Tích của hai số nguyên cùng dấu luôn là số nguyên dương.
3. Tính chất của phép nhân các số nguyên
Giống như phép nhân các số tự nhiên, phép nhân các số nguyên cũng có các tính chất sau:
– Giao hoán: a.b = b.a
– Kết hợp: a.(b.c) = (a.b).c
– Phân phối của phép nhân đối với phép cộng: a. (b+c) = a.b + a.c
– Phép nhân cũng có tính chất phân phối đối với phép trừ: a. (b-c) = a.b – a.c
E – Phép chia hết. Ước và bội của một số nguyên
Cho hai số nguyên a, b với b ≠ 0. Nếu có số nguyên q sao cho a = b.q thì ta nói:
- a chia hết cho b
- a là bội của b
- b là ước của a
Nếu a là bội của b thì –a cũng là bội của b.
Nếu b là ước của a thì –b cũng là ước của a.
Để tìm các ước của số nguyên a, ta tìm các ước dương của a cùng với các số đối của chúng.
II – Đề cương ôn thi học kì 1 Toán 6 sách mới | Hình học
Chương IV – Một số hình phẳng trong thực tế
A – Hình tam giác đều | Hình vuông | Hình lục giác đều
1. Tam giác đều
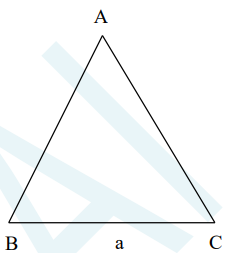
Tam giác đều là tam giác có:
– Ba cạnh bằng nhau.
– Ba góc ở các đỉnh bằng nhau và bằng 60°
2. Hình vuông

Dấu hiệu nhận biết ABCD là hình vuông:
– Bốn cạnh bằng nhau: AB = BC = CD = DA.
– Hai cạnh đối song song với nhau: AB song song với CD; AD song song với BC.
– Hai đường chéo bằng nhau: AC = BD.
– Bốn góc ở các đỉnh A, B, C, D bằng nhau và là góc vuông.
3. Lục giác đều
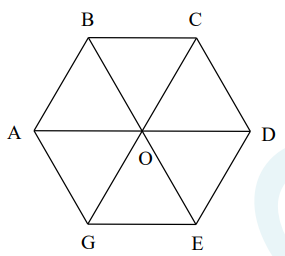
Lục giác đều ABCDEG có:
– Sáu cạnh bằng nhau: AB = BC = CD = DE = EG = GA.
– Ba đường chéo chính cắt nhau tại điểm O.
– Ba đường chéo chính bằng nhau: AD = BE = CG.
– Sáu góc ở các đỉnh A, B, C, D, E, G bằng nhau và bằng 120°
B – Hình chữ nhật | Hình thoi | Hình bình hành | Hình thang cân
1. Hình chữ nhật
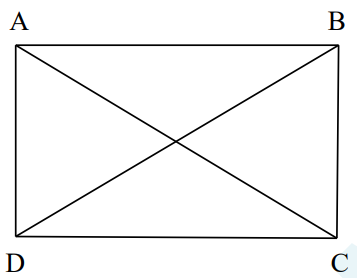
Hình chữ nhật ABCD có:
– Bốn đỉnh A, B, C, D.
– Hai cặp cạnh đối diện bằng nhau: AB = CD; BC = AD.
– Hai cặp cạnh đối diện song song: AB song song với CD; BC song song với AD.
– Bốn góc đỉnh A, B, C, D bằng nhau và bằng góc vuông.
– Hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường:
AC = BD; OA = OC; OB = OD.
2. Hình thoi
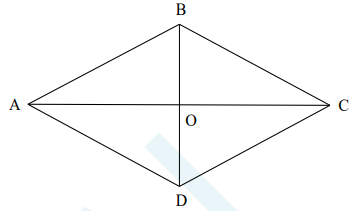
Hình thoi ABCD có:
– Bốn đỉnh A, B, C, D.
– Bốn cạnh bằng nhau: AB = BC = CD = DA.
– Hai cặp cạnh đối diện song song: AB song song với CD; BC song song với AD.
– Hai đường chéo AC và BD vuông góc với nhau.
3. Hình bình hành
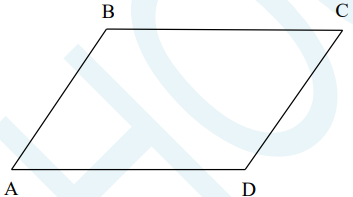
Hình bình hành ABCD có:
- Hai cặp cạnh đối diện song song: AB song song với CD; BC song song với AD.
- Hai cặp cạnh đối diện bằng nhau: AB = CD; BC = AD.
- Hai góc ở các đỉnh A và C bằng nhau, hai góc ở các đỉnh B và D bằng nhau.
- Hai đường chéo cắt nhau tại trung điểm mỗi đường.
4. Hình thang cân
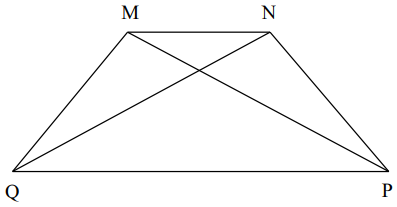
Hình thang cân MNPQ có:
– Hai cạnh đáy MN và PQ song song với nhau.
– Hai cạnh bên bằng nhau: MQ = NP; hai đường chéo bằng nhau: MP = NQ.
– Hai góc kề với cạnh đáy PQ bằng nhau, tức là hai góc NPQ và góc PQM bằng nhau; hai góc kề với cạnh đáy MN bằng nhau, tức là hai góc QMN và góc MNP bằng nhau.
C – Chu vi và diện tích của một số tứ giác đã học
1. Chu vi và diện tích của hình vuông
Chu vi của hình vuông có độ dài cạnh bằng a là
C = 4a
Diện tích của hình vuông có độ dài cạnh bằng a là:
S = a.a = a²
2. Chu vi và diện tích của hình chữ nhật
Cho hình chữ nhật có độ dài hai cạnh là a và b.
Chu vi hình chữ nhật đó là
C = 2(a+b)
Diện tích hình chữ nhật đó là
S = a.b
3. Chu vi và diện tích của hình thang cân
Chu vi của hình thang cân bằng tổng độ dài các cạnh của hình thang đó.
Diện tích của hình thang cân bằng tổng độ dài hai đáy nhân với chiều cao rồi chia đôi.
4. Chu vi và diện tích của hình bình hành
Cho hình bình hành có độ dài hai cạnh là a và b, độ dài đường cao ứng với cạnh a là h, ta có:
– Chu vi của hình bình hành là:
C = 2(a+b)
– Diện tích của hình bình hành là:
S = a.h
5. Chu vi và diện tích của hình thoi
Cho hình thoi có độ dài cạnh là a, độ dài hai đường chéo là m và n.
– Chu vi hình thoi đó là:
C = 4a
– Diện tích hình thoi đó là
S = ½.m.n
Chương V – Tính đối xứng của hình phẳng trong tự nhiên
A – Hình có trục đối xứng
1. Hình có trục đối xứng
Đường thẳng d chia hình H thành hai nửa. Nếu ta gấp theo đường thẳng d thì hai nửa này sẽ trùng khít vào nhau. Những hình như vậy gọi là hình có trục đối xứng và đường thẳng d được gọi là trục đối xứng của hình.
Hình có trục đối xứng còn được gọi là hình đối xứng trục.
2. Trục đối xứng của một số hình
– Đoạn thẳng AB là hình có trục đối xứng và trục đối xứng là đường thẳng d đi qua trung điểm O của đoạn thẳng AB và vuông góc với AB.
– Đường tròn là hình có nhiều trục đối xứng và mỗi trục đối xứng là một đường thẳng đi qua tâm của nó.
– Mỗi đường thẳng đi qua trung điểm hai cạnh đối diện là một trục đối xứng của hình chữ nhật.
– Hình thoi có trục đối xứng là hai đường chéo.
– Hình thang cân có 1 trục đối xứng là đường thẳng nối trung điểm của hai đáy. Hình lục giác đều có 6 trục đối xứng là các đường thẳng như hình sau:
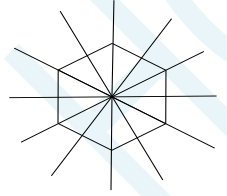
B – Hình có tâm đối xứng
1. Hình có tâm đối xứng
Hình có tâm đối xứng còn được gọi là hình đối xứng tâm.
2. Tâm đối xứng của một số hình
- Đoạn thẳng AB là hình có tâm đối xứng và tâm đối xứng là trung điểm của đoạn thẳng đó.
- Đường tròn là hình có tâm đối xứng và tâm đối xứng là tâm của nó.
- Hình thoi có tâm đối xứng là điểm O.
- Hình lục giác đều có tâm đối xứng là điểm O.
Có những hình có tâm đối xứng và có nhiều trục đối xứng.
⇒ Tham khảo ngay Đề cương ôn thi học kì 1 Toán 6 + Bài tập ôn luyện (có lời giải) đầy đủ 3 bộ sách theo chương trình mới tại đây:
- Đề cương ôn thi học kì 1 Toán 6 Cánh diều
- Đề cương ôn thi học kì 1 Toán 6 Kết nối tri thức
- Đề cương ôn thi học kì 1 Toán 6 Chân trời sáng tạo
III – ĐỀ THI CUỐI HỌC KÌ 1 TOÁN LỚP 6 THEO 3 BỘ SÁCH MỚI
Sau khi ôn luyện lại toàn bộ kiến thức lý thuyết đã học trong chương trình Toán lớp 6, các em hãy luyện tập với các đề thi để nắm chắc cũng như làm quen với ma trận đề thi. HOCMAI đã tổng hợp đầy đủ 3 bộ đề thi cuối học kì 1 Toán lớp 6 đầy đủ theo 3 bộ sách mới là Cánh Diều, Kết nối tri thức và Chân trời sáng tạo. Các em học sinh tham khảo ngay tại đây:
Tham khảo Đề thi học kì 1 Toán 6 Cánh Diều (Có hướng dẫn giải chi tiết) tại đây:
Tham khảo Đề thi học kì 1 Toán 6 Kết nối tri thức (Có hướng dẫn giải chi tiết) tại đây:
Tham khảo Đề thi học kì 1 Toán 6 Chân trời sáng tạo (Có hướng dẫn giải chi tiết) tại đây:
Trên đây là chi tiết về Đề cương ôn thi học kì 1 Toán 6 theo chương trình mới do HOCMAI biên soạn. Hy vọng với những kiến thức được tổng hợp cũng như các bộ đề thi ôn luyện cuối HK1 trong bài, các em học sinh sẽ nắm chắc kiến thức để đạt được kết quả cao khi tham gia kỳ thi chính thức.

















