A. Lý thuyết về phương trình bậc 2 1 ẩn
1. Định nghĩa:
Phương trình bậc 2 1 ẩn là phương trình có dạng:
AX² + BX + C = 0
Trong đó:
- a, b, c được gọi là các hệ số (a ≠ 0)
- x được gọi là ẩn
Ví dụ:
3x2 – 18x + 3 = 0 là phương trình bậc hai một ẩn trong đó a = 3; b = -18; c = 3
15x2 – 13x + 20 = 0 là phương trình bậc hai một ẩn trong đó a = 15; b = -13; c = 20.
6x2 – 10 = 0 là phương trình bậc hai một ẩn có a = 6; b = 0 và c = -10
9x2 + 20x = 0 là phương trình bậc hai một ẩn có a = 9 và b = 20; c = 0
2. Một số trường hợp của phương trình bậc 2 1 ẩn
Trường hợp 1: Khi ẩn số a = 0
Lúc này phương trình sẽ trở về dạng phương trình bậc nhất 1 ẩn có dạng bx + c = 0
Ta có nghiệm của phương trình: x = -c/b
Trường hợp 2: Khi ẩn số b = 0
Lúc này phương trình sẽ có dạng: ax² + c = 0
Ta có nghiệm của phương trình: x = ±√(-c/a)
Trường hợp 3: Khi ẩn số c = 0
Lúc này phương trình sẽ có dạng: ax² + bx = 0 ⇔ x(ax + b) = 0
Ta có 2 nghiệm của phương trình: x = 0 và x = -b/a
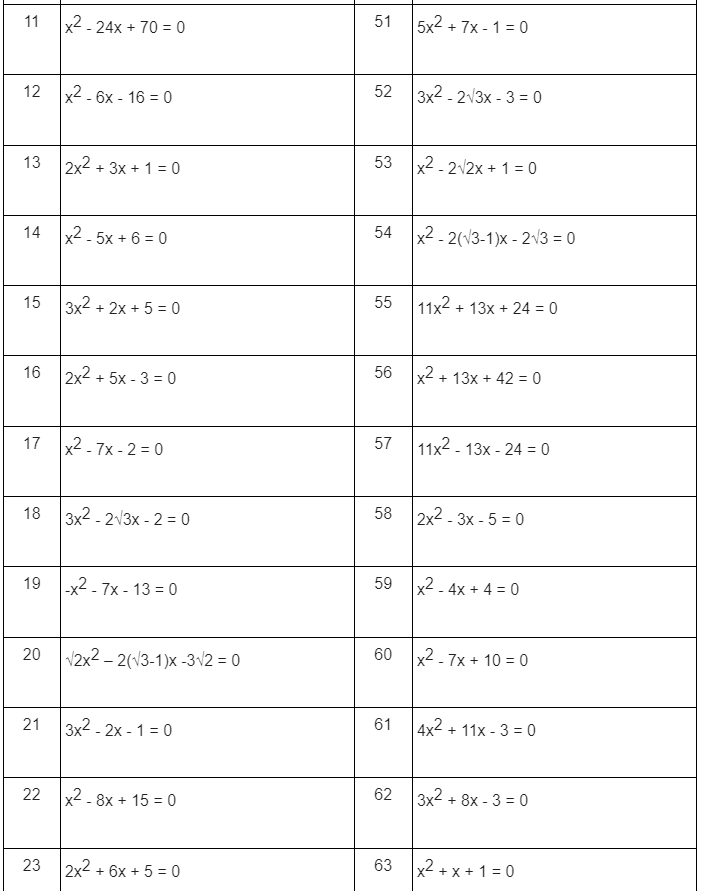
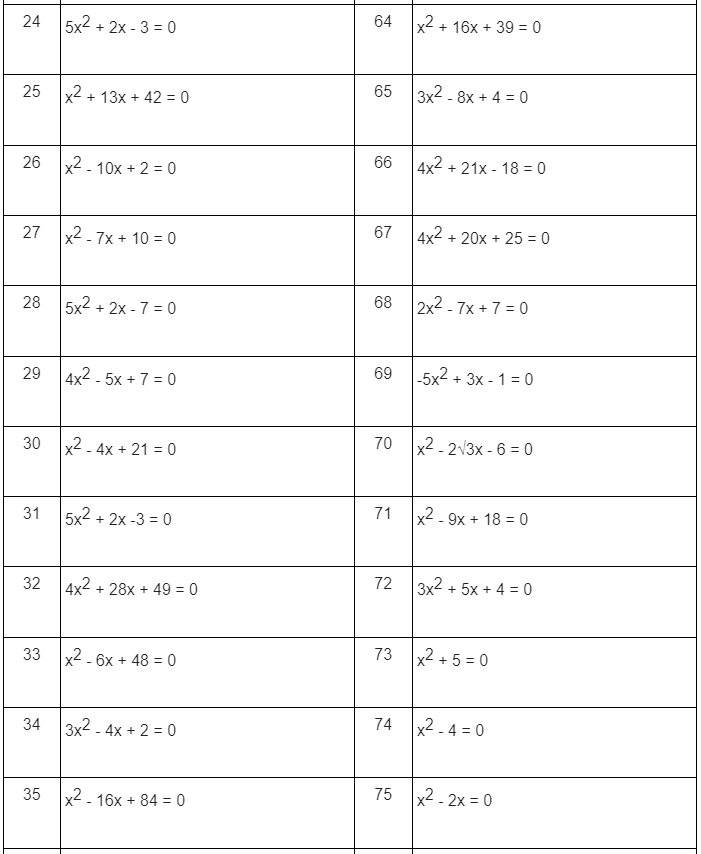
3. Một số dạng bài phương trình bậc 2 một ẩn

Lộ trình toàn diện - NẮM CHẮC NỀN TẢNG - TỔNG ÔN TOÀN DIỆN - LUYỆN ĐỀ CHUYÊN SÂU
ĐA DẠNG HÌNH THỨC HỌC - PHÙ HỢP VỚI MỌI NHU CẦU
TOP THẦY CÔ DANH TIẾNG, GIÀU KINH NGHIỆM
DỊCH VỤ HỖ TRỢ HỌC TẬP ĐÔNG HÀNH TRONG SUÔT QUÁ TRÌNH HỌC TẬP


Tham khảo thêm:
Trên đây là các kiến thức cơ bản cần nắm được về phương trình bậc 2 1 ẩn. Hy vọng bài viết trên sẽ giúp các em học sinh dễ dàng trong quá trình giải bài tập về chuyên đề nay trong chương trình Toán lớp 9 hay trong quá trình ôn thi môn toán vào lớp 10.


















