Tính chất của hai tiếp tuyến cắt nhau là phần kiến thức các em học sinh sẽ được học ở Toán học lớp 9. Đây là một trong những nội dung tương đối quan trọng để các em có thể ứng dụng giải các dạng bài tập toán hình học. Cùng HOCMAI ôn lại lý thuyết và những dạng bài tập liên quan trong bài viết sau.
I. Kiến thức cần nắm về Tính chất của hai đường tiếp tuyến cắt nhau
1. Định lý về hai tiếp tuyến cắt nhau
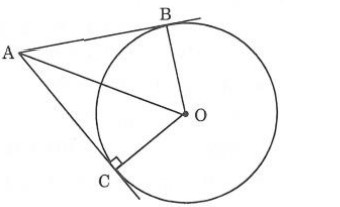
Định lý: Nếu hai tiếp tuyến của một đường tròn cắt nhau tại một điểm thì:
- Điểm đó cách đều hai tiếp điểm
- Tia kẻ từ điểm đó đi qua tâm đường tròn chính là tia phân giác của góc tạo bởi hai tiếp tuyến
- Tia được kẻ từ tâm đi qua điểm đó chính là tia phân giác của góc được tạo bởi hai bán kính đi qua các tiếp điểm.
2. Đường tròn nội tiếp tam giác
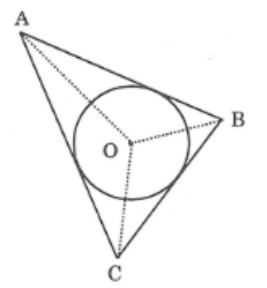
- Đường tròn tiếp xúc với cả ba cạnh của một tam giác được gọi là đường tròn nội tiếp tam giác, còn tam giác gọi là ngoại tiếp đường tròn.
- Tâm của đường tròn nội tiếp tam giác là giao điểm của các đường phân giác của góc trong của tam giác.
3. Đường tròn bàng tiếp
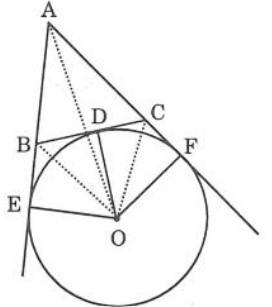
- Đường tròn tiếp xúc với một cạnh của tam giác và tiếp xúc với hai phần kéo dài của hai cạnh kia gọi là đường tròn bàng tiếp tam giác.
- Tâm đường tròn bàng tiếp tam giác trong góc A chính là giao điểm của hai đường phân giác các góc ngoài tại điểm B và điểm C, hoặc là giao điểm của đường phân giác góc trong A và đường phân giác góc ngoài tại B (hoặc C ). Trong một tam giác sẽ có ba đường tròn bàng tiếp.
II. Những dạng bài tập về Tính chất của hai tiếp tuyến cắt nhau
Dạng 1: Chứng minh các đường thẳng song song, vuông góc với nhau; chứng minh hai đoạn thẳng bằng nhau.
Để làm được dạng toán này, chúng ta sẽ sử dụng định lý tính chất của hai tiếp tuyến cắt nhau đã nêu ở trên.
Bài 1: Cho đường tròn tâm O. A là điểm nằm bên ngoài đường tròn đó. Kẻ các tiếp tuyến AB và AC với đường tròn ( với B,C là các tiếp điểm).
a) Chứng minh đoạn thẳng OA vuông góc với đoạn thẳng BC.
b) Vẽ đường kính CD. Chứng minh rằng BD // AO.
c) Tìm độ dài các cạnh của ΔABC, biết đoạn thẳng OB bằng 2cm; đoạn thẳng OA bằng 4cm.
Lời giải:
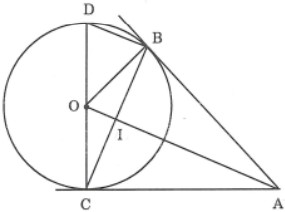
a) Chứng minh OA vuông góc BC.
Muốn chứng minh được AO vuông góc với BC thì ta phải chứng minh được ΔABC cân tại A.
ΔABC có: AB = AC vì AB và AC là hai tiếp tuyến của đường tròn (O) cắt nhau tại A nên theo định lý:
Nếu hai tiếp tuyến của một đường tròn cắt nhau tại một điểm thì nó cách đều hai tiếp điểm => ΔABC cân tại A (Tam giác có hai cạnh bằng nhau là tam giác cân) => Đường phân giác AO của góc BAC lại là đường cao ứng với đáy BC.
=> Vậy AO vuông góc với BC. (1)
b) Chứng minh rằng BD // AO.
ΔBCD có OB = OD = OC = CD/2 (đều là bán kính của đường tròn tâm O) => ΔBCD vuông tại B (Theo định lý: Nếu một tam giác có đường trung tuyến thuộc cạnh nào bằng nửa cạnh ấy thì tam giác đó là tam giác vuông)
=> BD vuông góc với BC (2)
Từ (1) và (2) => BD // AO.
c) Tìm độ dài các cạnh của ΔABC

Bài 2: Từ một điểm A nằm ngoài đường tròn tâm O, kẻ các tiếp tuyến AB và AC với đường tròn ( B,C là các tiếp điểm). Qua điểm M thuộc cung nhỏ BC kẻ tiếp tuyến với đường tròn tâm O, nó cắt các tiếp tuyến AB và AC theo thứ tự ở điểm D và điểm E. Chứng minh rằng chu vi ΔADE = 2AB.
Lời giải:
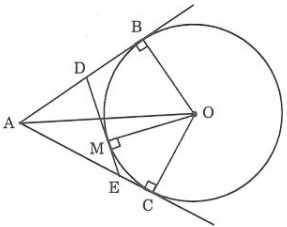
Muốn giải được bài này ta phải sử dụng định lý về tính chất hai tiếp tuyến cắt nhau.
Theo giả thiết ta có: DM = DB; EM = EC và AB = AC
=> Chu vi ΔADE là:
AD + DE + EA = AD + DM + EM + AE = AB + BD +EC + AE = 2AB (Vì AB = AC).
Dạng 2: Chứng minh đường thẳng là tiếp tuyến; tính độ dài; tính số đo góc và các yếu tố khác.
Để làm được dạng toán này, chúng ta sẽ sử dụng một trong phương pháp:
- Áp dụng định nghĩa tiếp tuyến; tính chất của hai tiếp tuyến cắt nhau.
- Áp dụng khái niệm đường tròn nội tiếp, bàng tiếp tam giác.
- Áp dụng hệ thức lượng về cạnh và góc trong một tam giác vuông.
Bài 1: Cho góc xAy không phải là góc bẹt. Điểm B thuộc tia Ax. Hãy dựng đường tròn tâm O tiếp xúc với đường thẳng Ax tại điểm B và tiếp xúc với đường thẳng Ay.
Lời giải:

Bài 2: Cho nửa đường tròn tâm O có đường kính là AB. Gọi Ax và By là các tia vuông góc với AB (Ax, By và nửa đường tròn thuộc cùng một nửa mặt phẳng bờ là AB). Qua điểm M thuộc nửa đường tròn ( M khác điểm A và điểm) kẻ tiếp tuyến với nửa đường tròn, cắt tia Ax và tia By theo thứ tự ở điểm C và điểm D.
a) Chứng minh góc COD là góc vuông.
b) Chứng minh CD = AC + BD.
c) Chứng minh Tích AC và BD không thay đổi khi điểm M di chuyển trên nửa đường tròn.
Lời giải:
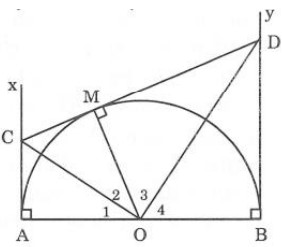
a) Chứng minh góc COD là góc vuông.

b) Chứng minh CD = AC + BD

Các bài viết tham khảo thêm:
Bài viết Tính chất của hai tiếp tuyến cắt nhau trên đã cung cấp cho các em học sinh kiến thức về lý thuyết cũng như những dạng bài tập và cách giải chi tiết. HOCMAI hy vọng đây sẽ là những thông tin bổ ích dành cho các em học và ôn tập chương trình Toán 9. Đừng quên truy cập hoctot.hocmai.vn thường xuyên để cập nhật những bài viết và thông tin mới nhất nhé!


















