Là một chương trong chương trình hình học Toán lớp 9, vị trí tương đối của đường thẳng và đường tròn là kiến thức nền tảng quan trọng giúp các em học sinh có thể áp dụng giải các bài tập sau này. Bài viết này HOCMAI sẽ giúp các em hiểu kỹ hơn về cả lý thuyết và một số bài tập có lời giải liên quan.
Bài viết tham khảo thêm:
Sự xác định đường tròn. Tính chất đối xứng của đường tròn
Đường kính và dây của đường tròn
I. Khái niệm đường thẳng và đường tròn
Trước khi tìm hiểu các kiến thức quan trọng về Vị trí tương đối của đường thẳng và đường tròn, chúng ta cần phải nắm chắc các kiến thức cơ bản về đường thẳng và đường tròn. Sau đây, HOCMAI sẽ nêu khái niệm cơ bản nhất về đường thẳng và đường tròn trong hình học phẳng.
Đường thẳng là gì?
Đường thẳng là không có định nghĩa cụ thể, nó là một trong những cơ sở sơ khai đầu tiên giúp xây dựng các khái niệm toán học khác. Có thể xem nó là một đối tượng không gian có đặc điểm: không có chiều rộng và không cong tại mọi điểm.
Một đường thẳng có thể hiểu như là một đường dài vô hạn, vô cùng mỏng và thẳng tuyệt đối. Trong hình học Euclid, chỉ có duy nhất một đường thẳng đi qua hai điểm bất kỳ khác nhau.
Đường tròn là gì?
Đường tròn là tập hợp của tất cả các điểm cách đều một điểm cho trước (điểm O) trên cùng một mặt phẳng. Đường tròn tâm O, bán kính R có ký hiệu là (O;R).
Sau khi hiểu rõ các khái niệm cơ về 2 yếu tố chính là đường thẳng và đường tròn. Chúng ta sẽ cùng nhau tìm hiểu ba loại vị trí tương đối giữa đường thẳng với đường tròn vào phần tiếp theo.
II. Lý thuyết về vị trí tương đối giữa đường thẳng với đường tròn
Hệ thức về vị trí tương đối giữa đường thẳng và đường tròn
Có 3 trường hợp về vị trí tương đối giữa đường thẳng với đường tròn là :
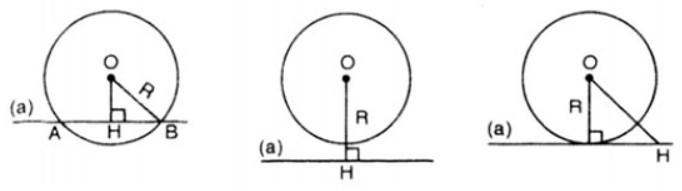
a) Đường thẳng và đường tròn có tiếp xúc, cắt nhau
Trường hợp đầu tiên trong 3 vị trí tương đối giữa đường thẳng với đường tròn. nó xảy ra khi một đường thẳng a bất kì cắt qua (O ; R) tại 2 điểm chung.
Gọi H là chân đường vuông góc nối từ tâm O vuông góc với đường thẳng a => OH là khoảng cách giữa tâm O và đường thẳng a.
b) Đường thẳng và đường tròn không tiếp xúc với nhau
Trường hợp này xảy ra khi đường thẳng và đường tròn không tiếp xúc với nhau (không có một điểm chung nào).
c) Đường thẳng và đường tròn tiếp xúc nhau tại một điểm
Trường hợp này xảy ra khi đường thẳng và đường tròn chỉ tiếp xúc tại duy nhất 1 điểm.
Gọi điểm C là điểm tiếp xúc của đường thẳng a trên (O;R) => OC là bán kính của đường tròn.
Từ 3 trường hợp vị trí tương đối giữa đường thẳng với đường tròn trên, ta có bảng hệ thức sau:
|
Vị trí tương đối của đường thẳng và đường tròn |
Số điểm chung |
Hệ thức giữa d và R |
|
Đường thẳng và đường tròn cắt nhau |
2 |
d < R |
| Đường thẳng và đường tròn tiếp xúc | 1 |
d = R |
| Đường thẳng và đường tròn không tiếp xúc | 0 |
d > R |
Trong đó: d là khoảng cách từ O đến đường thẳng a, R là bán kính đường tròn.
Nhận biết tiếp tuyến và tính chất của tiếp tuyến
a) Nhận biết tiếp tuyến
Nếu một đường thẳng đi qua một điểm trên đường tròn và vuông góc với bán kính đi qua điểm đó => đường thẳng ấy là một tiếp tuyến của đường tròn đó.
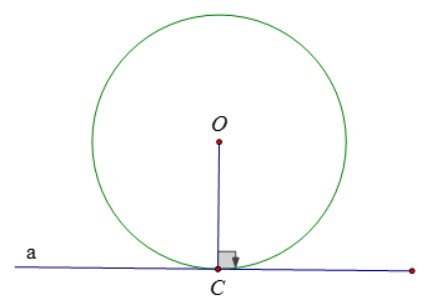
b) Tính chất của tiếp tuyến
- Nếu một đường thẳng là tiếp tuyến của đường tròn thì đường thẳng đó vuông góc với bán kính đi qua tiếp điểm ấy.
- Nếu có một đường thẳng đi qua một điểm của đường tròn và vuông góc với bán kính đi qua điểm đó thì nó là một tiếp tuyến của đường tròn.
Tính chất của hai tiếp tuyến cắt nhau
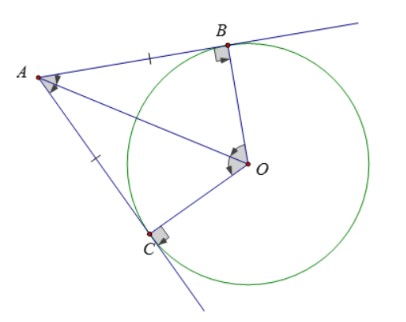
Nếu AB và AC là hai tiếp tuyến và cắt nhau tạo A thì:
- AB = AC
- góc BAO = góc COA
- góc COA = góc BOA
Đường tròn nội tiếp tam giác
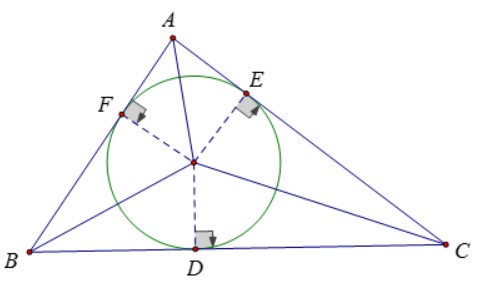
- Đường tròn nội tiếp tam giác là đường tròn tiếp xúc với cả ba cạnh của một tam giác. Tam giác thì được gọi là ngoại tiếp đường tròn.
- Giao điểm các đường phân giác của các góc trong tam giác là tâm đường tròn nội tiếp tam giác.
Đường tròn bàng tiếp tam giác
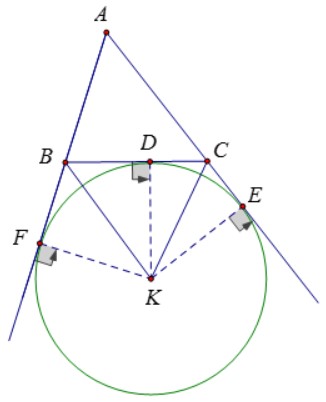
- Đường tròn có tiếp xúc với một cạnh của tam giác và tiếp xúc với các phần kéo dài của hai cạnh còn lại được gọi là đường tròn bàng tiếp tam giác.
- Có tất cả ba đường tròn bàng tiếp ở mỗi tam giác.
III. Các dạng bài tập về Vị trí tương đối của đường thẳng và đường tròn thường gặp
Dạng 1: Nhận biết vị trí tương đối của đường thẳng và đường tròn.
Bài 1: Cho (O ; R), gọi khoảng cách từ tâm O đến đường thẳng a là d. Hoàn thành bảng sau:

Lời giải:

Dạng 2: Bài tập vận dụng tính chất tiếp tuyến
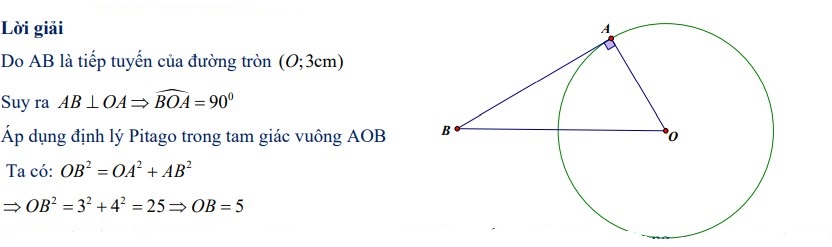
Bài 1: Cho điểm A thuộc đường tròn (O ; 3cm). Trên tiếp tuyến tại A của đường tròn (O), lấy điểm B sao cho AB = 4cm. Tính độ dài đoạn thẳng OB?
Bài 2: Cho ΔABC cân (AB = AC) nội tiếp đường tròn (O). Chứng minh rằng: BC // với tiếp tuyến tại A của đường tròn (O).

Dạng 3: Chứng minh tiếp tuyến của một đường tròn
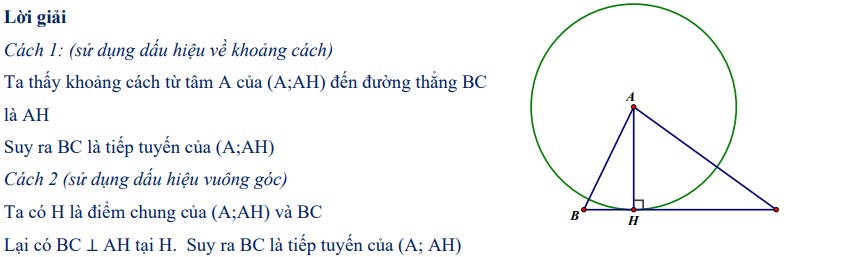
Bài 1: Cho ΔABC và đường cao AH. Chứng minh rằng BC là tiếp tuyến của đường tròn tâm A bán kính AH.
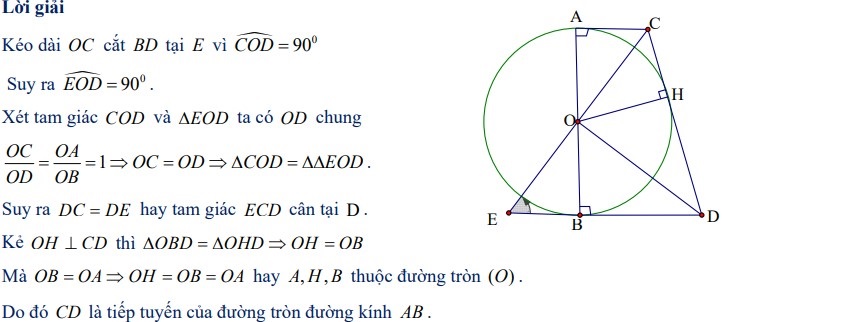
Bài 2: Cho hình thang vuông ABCD (vuông tại A và B) có O là trung điểm của AB và góc COD vuông. Chứng minh rằng CD là tiếp tuyến của đường tròn có đường kính AB.
Dạng 4: Bài tập nâng cao
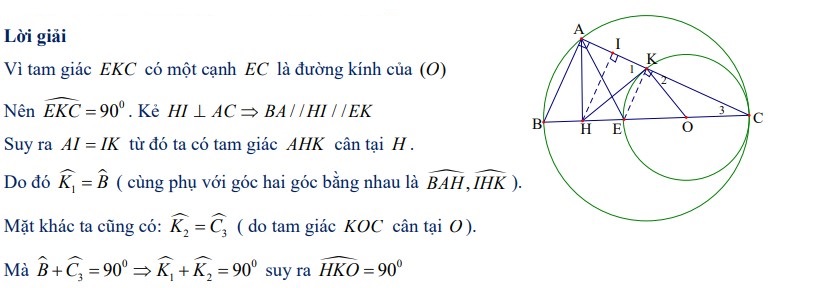
Bài 1: Cho ΔABC vuông tại A (AB < AC), đường cao AH. E là điểm đối xứng của điểm B qua H. Vẽ đường tròn đường kính EC cắt đoạn thẳng AC tại điểm K. Xác định vị trí tương đối của đoạn thẳng HK với đường tròn đường kính EC.
Bài viết trên HOCMAI đã khái quát những kiến thức cơ bản để tạo nên nên các trường hợp tương giao giữa đường thẳng và đường tròn. Mong rằng bài viết về vị trí tương đối của đường thẳng và đường tròn này sẽ giúp cho các em học sinh hiểu rõ hơn về bài học và biết cách ứng dụng để làm tốt bài tập của mình.





















