Góc có đỉnh ở bên trong đường tròn. Góc có đỉnh ở bên ngoài đường tròn trong hình học là kiến thức quan trọng trong chương trình học Toán lớp 9. Để hiểu rõ hơn về khái niệm, định lý và các dạng bài tập liên quan về kiến thức này. Các em học sinh hãy cùng HOCMAI tham khảo bài viết này nhé!
Bài viết tham khảo thêm:
I. Lý thuyết Góc có đỉnh ở bên trong đường tròn. Góc có đỉnh ở bên ngoài đường tròn
1. Góc có đỉnh ở bên trong đường tròn
a) Định nghĩa
Góc có đỉnh ở bên trong đường tròn là góc có đỉnh là giao điểm của hai dây cung và giao điểm này nằm bên trong đường tròn.
Hai cung nằm ở bên trong góc gọi là hai cung bị chắn.
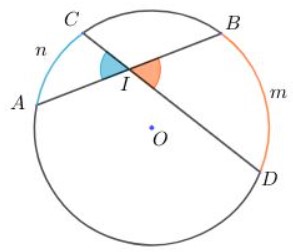
Góc BID và góc AIC cí đỉnh I nằm bên trong đường tròn. Hai cung AnC và cung BmD là hai cung bị chắn.
b) Định lý
Số đo của góc có đỉnh nằm bên trong đường tròn bằng một nửa (1/2) tổng số đo hai cung bị chắn.
Chứng minh định lý:
Xét đường tròn tâm A và góc I2 là góc có đỉnh ở trong đường tròn chắn hai cung AB và cung CD. Ta cần chứng minh:
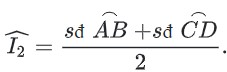
Ký hiệu các góc và các cung như trên hình vẽ:
Khi đó góc I2 là góc ngoài của tam giác IBC tại đỉnh I. Vì mỗi góc ngoài của một tam giác bằng tổng hai góc không kề với nó. Nên ta có:
Góc I2 = Góc B + góc C (1)
Lại có:
- Góc B là góc nội tiếp chắn cung CmD => Góc B = 1/2 số đo cung CmD.
- Góc C là góc nội tiếp chắn AnB => Góc C = 1/2 số đo cung AnB.
Thay vào (1) ta được:
Góc I2 = 1/2 số đo cung CmD + 1/2 số đo cung AnB
⇔ Góc I2 = (Số đo cung CmD + số đo cung AnB)/2
Vậy Góc I2 = (Số đo cung AB + số đo cung CD)/2 (ĐPCM)
2. Góc có đỉnh nằm ở bên ngoài đường tròn
a) Định nghĩa
Góc có đỉnh nằm ở bên ngoài đường tròn là góc có đỉnh là giao điểm của hai dây cung (Hoặc tiếp tuyến) và giao điểm này nằm ở bên ngoài đường tròn.
Hai cung nằm ở bên trong góc gọi là hai cung bị chắn.
b) Định lý
Số đo của góc có đỉnh ở bên ngoài đường tròn bằng một nửa (1/2) hiệu số đo hai cung bị chắn.
Chứng minh định lý:
Để chứng minh định lý trên, ta sẽ xét qua 3 trường hợp:
a) Mỗi cạnh của góc cắt đường tròn tại hai điểm phân biệt
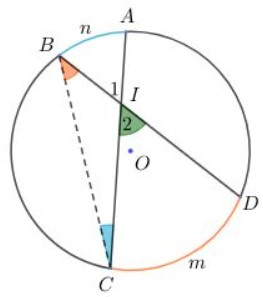
Xét góc A có đỉnh ở bên ngoài đường tròn tâm O chắn hai cung BD và cung CE. Ta cần chứng minh:
Góc A = (Số đo cung BD + số đo cung CE)/2
Ký hiệu và các cung như hình vẽ sau:
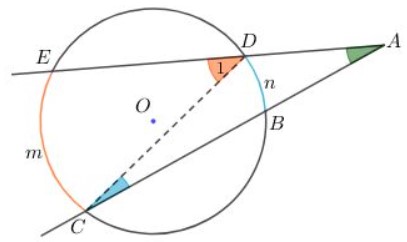
Ta có góc D1 là góc ngoài tại đỉnh D của tam giác ADC nên:
Góc D1 = Góc C + góc A => Góc A = Góc D1 – Góc C (1)
Lại có:
- Góc D1 là góc nội tiếp chắn cung CmE => Góc D1 = 1/2 số đo cung CmE.
- Góc C là góc nội tiếp chắn cung BnD => Góc C = 1/2 số đo cung BnD.
Thay vào (1) ta được:
Góc A = 1/2 số đo cung CmE – 1/2 số đo cung BnD
=> Góc A = (Số đo cung CmE – số đo cung BnD)/2
Vậy Góc A = (Số đo cung BD – số đo cung CE)/2 (ĐPCM)
b) Một cạnh của góc tiếp tuyến của đường tròn
Xét góc A có đỉnh ở bên ngoài đường tròn tâm O và một cạnh AB là tiếp tuyến chắn hai cung CB và cung BD. Ta cần chứng minh:
Góc A = (Số đo cung CB + số đo cung BD)/2
Ký hiệu và các cung như hình vẽ sau:
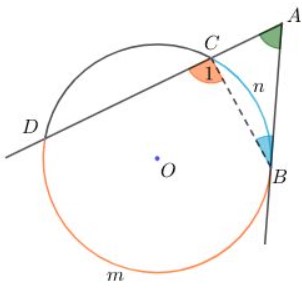
Ta có góc C1 là góc ngoài tại đỉnh C của tam giác ADC nên:
Góc C1 = Góc A + góc B => Góc A = Góc C1 – Góc B (2)
Lại có:
- Góc C1 là góc nội tiếp chắn cung BmD => Góc C1 = 1/2 số đo cung BmD.
- Góc B là góc tạo bởi tiếp tuyến BA và dây cung BC chắn cung BnC => Góc B = 1/2 số đo cung BnC.
Thay vào (2) ta được:
Góc A = 1/2 số đo cung BmD – 1/2 số đo cung BnC
=> Góc A = (Số đo cung BmD – số đo cung BnC)/2
Vậy Góc A = (Số đo cung CB – số đo cung BD)/2 (ĐPCM)
c) Hai cạnh của góc là hai tiếp tuyến của đường tròn
Xét góc A có đỉnh ở bên ngoài đường tròn tâm O và hai cạnh là hai tiếp tuyến của đường tròn tâm O. Ký hiệu và các cung như hình vẽ sau:
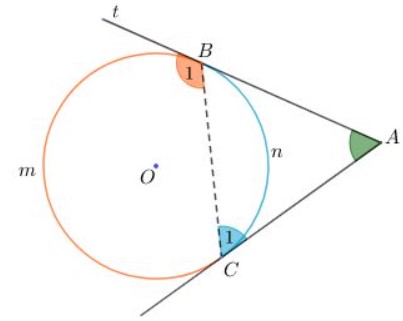
Khi đó góc A chắn cung BmC và cung nhỉ BnC. Ta cần chứng minh:
Góc A = (Số đo cung BC + số đo cung BC)/2
Ta có góc B1 là góc ngoài tại đỉnh C của tam giác ADC nên:
Góc B1 = Góc C1 + góc A => Góc A = Góc B1 – Góc C1 (3)
Lại có:
- Góc B1 là góc tạo bởi tiếp tuyến Bt và dây cung BC chắn cung lớn BmC
=> Góc B1 = 1/2 số đo cung BmC.
- Góc C1 là góc tạo bởi tiếp tuyến CA và dây cung CB chắn cung nhỏ CnB
=> Góc C1 = 1/2 số đo cung CnB.
Thay vào (3) ta được:
Góc A = 1/2 số đo cung BmC – 1/2 số đo cung CnB
=> Góc A = (Số đo cung BmC – số đo cung CnB)/2
Vậy Góc A = (Số đo cung BC + số đo cung BC)/2 (ĐPCM)
II. Bài tập Góc có đỉnh ở bên trong đường tròn. Góc có đỉnh ở bên ngoài đường tròn
Dạng 1 – Chứng minh hai góc – Hai đoạn thẳng bằng nhau
Giải bằng phương pháp: Sử dụng 2 định lý về số đo của góc có đỉnh ở bên trong đường tròn, góc có đỉnh bên.
Ví dụ: Cho tam giác ABC nội tiếp đường tròn tâm O. Các tia phân giác của góc B và góc C cắt nhau tại điểm I và cắt đường tròn (O) lần lượt tại điểm D và điểm E. Dây DE cắt các cạnh AB và cạnh AC lần lượt tại điểm M và điểm N. Chứng minh:
a) Ba tam giác AMN, ΔEAI và ΔDAI là tam giác cân;
b) Tứ giác AMIN là một hình thoi.
Lời giải:
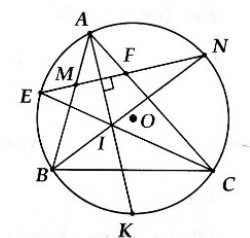
a) Góc AMN = Góc ANM = 1/2 số đo cung ED
=> AMN cân tại A.
Kéo dài AI cắt đường tròn (O) tại điểm K. Chứng minh tương tự, ta có ΔAIE và ΔDIA lần lượt là tam giác cân tại E và D.
b) Xét ΔAMN cân tại A có AI là phân giác.
=> AI ⊥ MN tại F và MF = FN.
Tương tự với ΔEAI cân tại E, ta có: AF = IF.
=> Tứ giác AMIN là một hình hình hành. Mà AI ⊥ MN => AMIN là hình thoi (ĐPCM).
Dạng 2 – Chứng minh hai đường thẳng song song, vuông góc với nhau. C/minh các đẳng thức cho trước
Phương pháp giải: Áp dụng, sử dụng 2 định lý về số đo của góc có đỉnh bên trong đường tròn, góc có đỉnh bên ngoài đường tròn để có tìm được các góc bằng nhau, cạnh bằng nhau. Từ đó, ta tìm được điều cần chứng minh.
Ví dụ: Cho ΔABC nội tiếp đường tròn (O). Các tia phân giác của các góc A và góc B cắt nhau tại điểm I và cắt đường tròn theo thứ tự ở điểm D và E. Chứng minh:
a) Tam giác BDI là một tam giác cân;
b) DE chính là đường trung trực của IC;
c) IF // BC, trong đó F chính là giao điểm của DE và AC.
Lời giải:
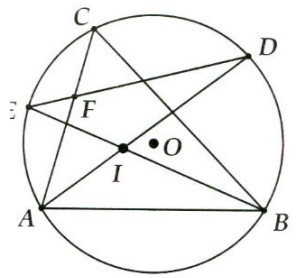
a) Góc BID = 1/2 Số đo cung DE = Góc DBE => Tam giác BDI cân tại D.
b) Chứng minh tương tự câu a, ta có ΔIEC cân tại E, ΔDIC cân tại D.
=> EI = EC và DI = DC
=> DE là trung trực của CI.
c) F ∈ DE nên FI = FC
=> Góc FIC = Góc FCI = Góc ICB
=> IF // BC
Bài tập trắc nghiệm về góc có đỉnh ở bên trong đường tròn – Góc có đỉnh ở bên ngoài đường tròn luyện tập phản xạ.
Câu 1: Cho hình vẽ dưới đây, góc BIC có số đo bằng:
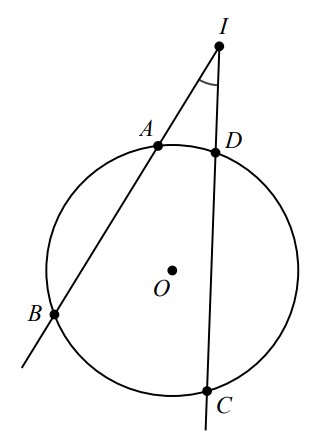
A. (Số đo cung BC + số đo cung AD)/2
B. (Số đo cung BC – số đo cung AD)/2
C. (Số đo cung AB + số đo cung CD)/2
D. (Số đo cung AB – số đo cung CD)/2
Lời giải:
Số đo của góc có đỉnh ở bên ngoài đường tròn bằng một nửa hiệu số đo hai cung bị chắn:
Góc BIC = (Số đo cung BC – số đo cung AD)/2
Vậy đáp án cần chọn là B.
Câu 2: Góc có đỉnh nằm ở bên ngoài đường tròn có số đo:
A. Bằng một nửa hiệu số đo hai cung bị chắn.
B. Bằng một nửa tổng số đo hai cung bị chắn.
C. Bằng số đo của cung lớn bị chắn.
D. Bằng số đo của cung nhỏ bị chắn.
Lời giải:
Số đo của góc có đỉnh nằm bên ngoài đường tròn bằng một nửa hiệu số đo hai cung bị chắn.
Vậy đáp án cần chọn là A.
Câu 3: Cho một nửa đường tròn tâm O, đường kính AB và C là điểm nằm trên cung nhỏ AB (cung CB nhỏ hơn cung CA). Tiếp tuyến tại điểm C của nửa đường tròn cắt đường thẳng AB tại điểm D . Biết tam giác ADC cân tại C. Tính góc ADC.
A. 40°.
B. 45°.
C. 60°.
D. 30°.
Lời giải:
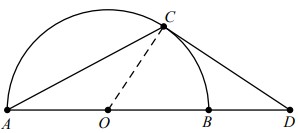
Xét nửa đường tròn ta có:
- Góc BAC = 1/2 số đo cung BC
- Góc CAD = 1/2 (số đo cung AC – số đo cung BC)
- Tam giác ADC cân tại C nên góc DAC = góc CDA ⇔ Số đo cung BC = Số đo cung AC – số đo cung BC
Từ đó suy ra: Số đo cung BC = Số đo cung AC
Mà Số đo cung AC + Số đo cung BC = 180° => Số đo cung AC = 120°; số đo cung BC = 60°
=> Góc ADC = 30°
Vậy đáp án cần chọn là D.
Cây 4: Trên (O) lấy bốn điểm A, B, C, D theo thứ tự sao cho số đo cung AB = số đo cung BC = số đo cung CD. Gọi giao điểm của BD và AC là I, biết góc BIC bằng 70°. Tính góc ABD.
A. 20.
B. 15.
C. 35.
D. 30.
Lời giải:
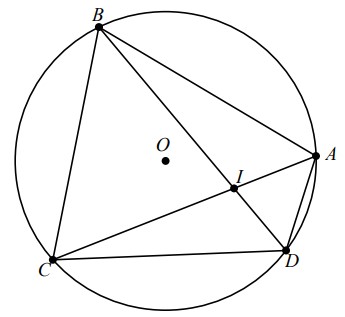
Vì số đó cung AB = số đo cung BC = số đo cung CD nên gọi cung là a độ. Ta có số đo cung AD là: 360° – 3a
Vì góc BIC là góc có đỉnh nằm ở bên trong đường tròn nên:
Góc BIC = (a + 360° – 3a)/2 = 70° => a = 110°
=> Số đo cung AD là: 360° – 3a = 360° – 3.110° = 30°
Góc ABD là góc nội tiếp chắn cung AD => Góc ABD = 30°/2 = 15°
Vậy đáp án cần chọn là B.
(Hết)
Bài viết trên đã cung cấp kiến thức cho các em học sinh về Góc có đỉnh ở bên trong đường tròn. Góc có đỉnh ở bên ngoài đường tròn Toán hình học lớp 9. Hy vọng rằng đây sẽ là những kiến thức bổ ích giúp cho các em học tập hiệu quả và dễ dàng giải các bài toán liên quan đến kiến thức này.


















