Đề cương Ôn thi học kì 1 môn Toán lớp 8 chi tiết (Kèm đề thi ôn tập)

Đề cương Ôn thi học kì 1 môn Toán lớp 8 là bài viết do HOCMAI sưu tầm, tổng hợp và hệ thống kiến thức lại kiến thức Toán học kì 1 lớp 8 để gửi tới các em học sinh. Các em sẽ cùng HOCMAI tổng ôn lại tất cả những kiến thức trọng tâm, một số dạng bài thường gặp và luyện tập bằng các đề ôn thi học kì 1 lớp 8 môn toán dưới đây nhé!

 

Bài viết tham khảo thêm: Đề cương ôn thi giữa học kì 1 toán 8

 

I – KIẾN THỨC TRỌNG TÂM ÔN THI HỌC KÌ 1 TOÁN 8

A – PHẦN ĐẠI SỐ

CHƯƠNG 1: PHÉP NHÂN VÀ PHÉP CHIA CÁC ĐA THỨC

1. Nhân đơn thức với đa thức

Muốn nhân một đơn thức cùng với một đa thức, ta nhân đơn thức cùng với từng số hạng của đa thức rồi cộng các tích lại với nhau.

VD: Cho A, B, C, D là các đơn thức, ta có: A.(B + C – D) = AB + AC – AD

2. Nhân đa thức với đa thức 

Muốn nhân một đa thức cùng với một đa thức, ta đem nhân mỗi hạng tử của đa thức này với từng hạng tử của đa thức kia rồi sau đó cộng các tích lại với nhau.

VD: Cho A, B, C, D là các đa thức, ta có:

(A + B).(C+D) = A(C + D) + B.(C + D) = AC + AD + BC + BD

→ Nắm vững quy tắc nhân đơn thức với đa thức, nhân đa thức với đa thức TẠI ĐÂY!

3. Những hằng đẳng thức đáng nhớ

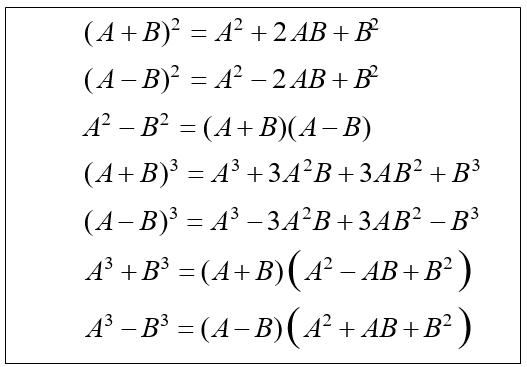
4. Phân tích đa thức thành nhân tử

• Phương pháp đặt nhân tử chung
• Phương pháp sử dụng hằng đẳng thức
• Phương pháp nhóm hạng tử
• Phối hợp nhiều phương pháp

Tham khảo thêm các phương pháp phân tích đa thức thành nhân tử Tại đây!

5. Chia đơn thức cho đơn thức

Quy tắc: Để chia đơn thức A cho đơn thức B (trường hợp mà A chia hết cho B) thì ta làm như sau:

• Chia hệ số của đơn thức A cho hệ số của đơn thức B.
• Chia lũy thừa của từng biến trong hệ thức A cho lũy thừa của cùng biến đó trong hệ thức B.
• Nhân các kết quả vừa tìm được lại với nhau.

6. Chia đa thức cho đơn thức

Quy tắc: Để chia đa thức A cho đơn thức B (trường hợp mà các hạng tử của đa thức A đều chia hết được cho đơn thức B) ta chia mỗi hạng tử của A cho B sau đó cộng các kết quả lại với nhau.

7. Chia đa thức một biến đã sắp xếp

Quy tắc: Ta trình bày phép chia tương tự như cách chia các số tự nhiên. Với hai đa thức một biến A và B, B ≠ 0 tồn tại duy nhất hai đa thức Q và R sao cho: A = B.Q + R với R = 0 hoặc R ≠ 0 có bậc bé hơn bậc của B.

• Nếu R = 0 → Ta được phép chia hết.
• Nếu R  ≠ 0 → Ta được phép chia có dư.

CHƯƠNG 2: PHÂN THỨC ĐẠI SỐ

1. Khái niệm về phân thức đại số và tính chất của phân thức đại số

a) Phân thức đại số là biểu thức có dạng A/B với A, B là những đa thức và B ≠ 0

b) Hai phân thức bằng nhau: A/B = C/D nếu A.D = B.C

c) Tính chất cơ bản của phân thức: 

Nếu M ≠ 0 thì:

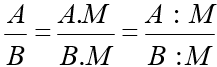
2. Các phép toán trên tập hợp các phân thức đại số

a) Phép cộng

• Cộng hai phân thức có cùng mẫu thức:

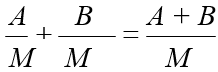
• Cộng hai phân thức khác (không cùng) mẫu thức:

– Quy đồng mẫu thức.

– Cộng hai phân thức có cùng mẫu thức ta vừa tìm được.

b) Phép trừ

+) Phân thức đối của A/B ký hiệu bởi – A/B

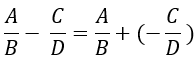
c) Phép nhân

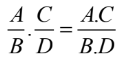
d) Phép chia

+ Phân thức nghịch đảo của phân thức A/B ≠ 0 là B/A

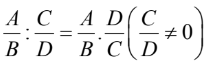
B – PHẦN HÌNH HỌC

CHƯƠNG 1: TỨ GIÁC

1. Định nghĩa, tính chất và những dấu hiệu để nhận biết các hình

Hình	Định nghĩa	Tính chất	Dấu hiệu nhận biết
Tứ giác	Là một đa giác hình gồm có 4 cạnh và 4 đỉnh, trong đó sẽ không có bất kì 2 đoạn thẳng nào cùng nằm ở trên một đường thẳng	∠A + ∠B + ∠C + ∠D = 360º
Hình thang	Là một tứ giác lồi có hai cạnh đối diện song song với nhau	∠A + ∠D = ∠C + ∠B = 180º	Tứ giác có AB//CD
Hình thang vuông	Hình thang có 1 góc bằng 90º	∠A = ∠D = 90º ∠B + ∠C = 180º	Hình thang có 1 góc bằng 90º
Hình thang cân	Là hình thang có hai góc kề 1 đáy bằng với nhau.	– Hai góc kề 1 đáy bằng nhau: ∠A = ∠B; ∠C = ∠D – Hai đường chéo bằng với nhau: BD = AC – Hai cạnh bên bằng với nhau: BC = AD	+ Hai góc kề 1 đáy bằng nhau: ∠A = ∠B hoặc ∠C = ∠D. + Hai đường chéo bằng với nhau: AC = BD.
Hình bình hành	Tứ giác có các cạnh đối diện song song cùng với nhau.	– AB = CD; AD = BC. – ∠A = ∠C; ∠B = ∠D  – I là trung điểm của cạnh AC và cạnh BD.	+ Các cạnh đối song song. + Các cạnh đối bằng nhau. + Hai cạnh đối song song và bằng nhau.   + Các góc đối bằng nhau. + Hai đường chéo cắt nhau ở trung điểm của từng đường.
Hình chữ nhật	Tứ giác có 4 góc vuông	– Tất cả những tính chất của hình thang cân và hình bình hành – Hai đường chéo bằng với nhau và cắt nhau ở trung điểm mỗi đường	+ Tứ giác có 3 góc vuông. + Là hình thang cân có 1 góc vuông. + Là hình bình hành có 1 góc vuông. + Là hình bình hành có 2 đường chéo bằng với nhau.
Hình thoi	Tứ giác có 4 cạnh bằng nhau	+ Hai đường chéo ⊥ cùng với nhau. + Hai đường chéo là những đường phân giác của các góc trong hình thoi và cắt nhau ở trung điểm của mỗi đường + Tất cả những tính chất của một hình bình hành	+ Tứ giác có 4 cạnh bằng nhau. + Hình bình hành có hai cạnh kề bằng nhau. + Hình bình hành có hai đường chéo ⊥ cùng với nhau. + Hình bình hành có 1 đường chéo chính là đường phân giác của một góc.
Hình vuông	Tứ giác có 4 góc vuông và	Có tất cả những tính chất của hình chữ nhật, hình thoi	+ Hình chữ nhật có hai cạnh kề bằng với nhau. + Hình chữ nhật có hai đường chéo ⊥ với nhau. + Hình chữ nhật có một đường chéo chính là đường phân giác của một góc. + Hình thoi có 1 góc vuông. + Hình thoi có 2 đường chéo bằng với nhau.

 

2. Đường trung bình của tam giác, hình thang

Đường trung bình của	Định nghĩa	Định lý
Tam giác	Là đoạn thẳng nối trung điểm hai cạnh của tam giác	+ Đường thẳng đi qua trung điểm một cạnh của tam giác và song song với cạnh thứ hai thì đi qua trung điểm cạnh thứ ba của tam giác. + Đường trung bình của tam giác song song cùng với cạnh thứ ba và bằng một nửa cạnh ấy.
Hình thang	Là đoạn thẳng nối trung điểm hai bên của hình thang	+ Đường thẳng đi qua trung điểm một cạnh bên của hình thang và song song với hai cạnh đáy thì đi qua trung điểm cạnh bên thứ hai. + Đường trung bình của hình thang song song cùng với hai đáy và bằng một nửa tổng hai đáy.

 

CHƯƠNG 2: ĐA GIÁC. DIỆN TÍCH ĐA GIÁC

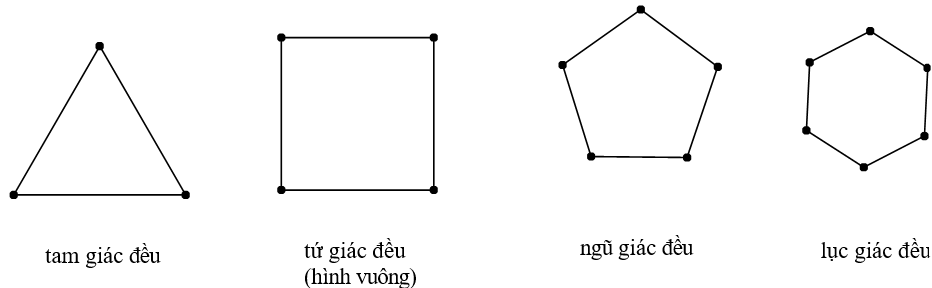
1. Đa giác đều: Là đa giác có tất cả các cạnh bằng với nhau và tất cả các góc bằng với nhau.

Ví dụ:

2. Diện tích đa giác

Đa giác	Công thức tính diện tích
Hình chữ nhật	S = a.b
Hình vuông	S = a²
Hình tam giác	S = 1/2a.b
Hình thang	S = 1/2.h.(a+b)
Hình bình hành	S = a.h
Hình thoi	S = 1/2a.b

II – MỘT SỐ DẠNG BÀI THƯỜNG GẶP – ÔN THI HỌC KÌ 1 TOÁN 8

A. Đại số

1. Thực hiện phép tính với đa thức, đơn thức. Rút gọn và tính giá trị của biểu thức

Phương pháp: Thực hiện nhân, chia theo quy tắc đã học, chú ý về dấu:

– Nếu trước dấu ngoặc là dấu “ ” thì khi nhân vào bỏ dấu ngoặc sẽ giữ nguyên dấu.

– Nếu trước dấu ngoặc là dấu “ ” thì khi nhân vào bỏ dấu ngoặc phải đổi dấu tất cả.

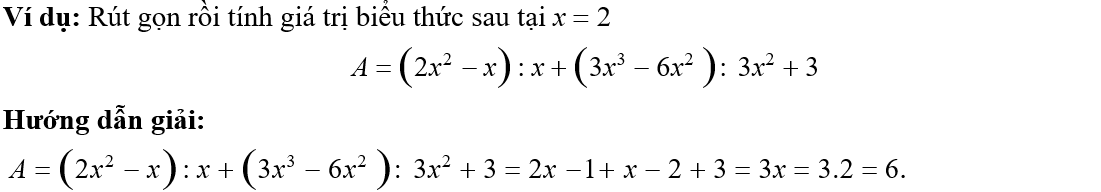
2. Phân tích đa thức thành nhân tử

Phương pháp: Sử dụng một trong các phương pháp đã học.

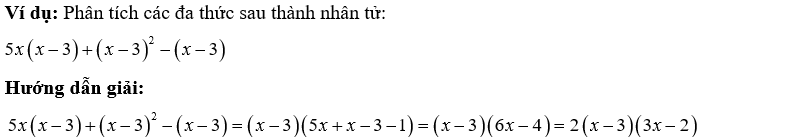
3. Chia đa thức cho đơn thức, chia hai đa thức

Phương pháp:

– Chia đa thức cho đơn thức: Để chia đa thức A cho đơn thức B, ta chia mỗi hạng tử của A cho B sau đó cộng các kết quả lại với nhau (Với điều kiện là các hạng tử của đa thức A đều chia hết được cho đơn thức B).

– Chia đa thức cho đa thức: Đặt tính chia tương tự cách chia các số tự nhiên.

Với hai đa thức A và B của một biến, B ≠ 0 tồn tại duy nhất đa thức Q và R sao cho: 

A = B.Q + R 

+) R = 0 → Phép chia là phép chia hết.

+) R  ≠ 0 (bậc của R nhỏ hơn bậc của B) → Phép chia là phép chia có dư.

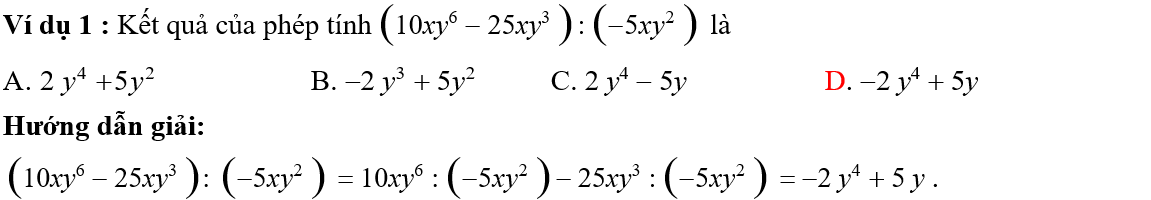
4. Tìm điều kiện để phân thức xác định

Phương pháp: Phân thức Ax/Bx xác định khi Bx ≠ 0

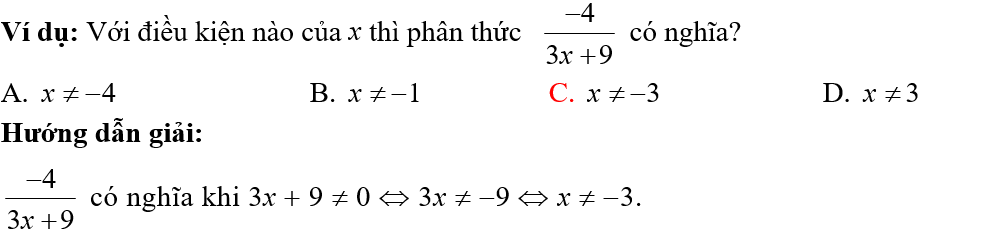
5. Thực hiện các phép tính với phân thức

Phương pháp: Thực hiện cộng, trừ, nhân, chia các phân thức như cách cộng, trừ, nhân, chia các phân số. Chú ý áp dụng kĩ năng phân thức đa thức thành nhân tử để rút gọn phân thức trong quá trình làm.

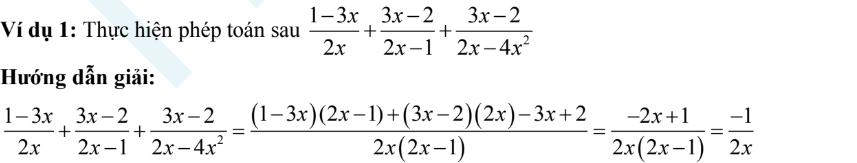
6. Tính giá trị biểu thức (chứa phân thức) tại giá trị cho trước của biển

Phương pháp:

Bước 1: Tìm điều kiện để các phân thức xác định. Nếu giá trị cho trước của biến làm cho một trong các phân thức không xác định thì kết luận không tồn tại giá trị của biểu thức thỏa mãn còn không thì tiếp tục bước 2.

Bước 2: Rút gọn biểu thức (thực hiện phép tính với đa thức, phân thức).

Bước 3: Thay giá trị cho trước của biến vào biểu thức và thực hiện phép tính với số.

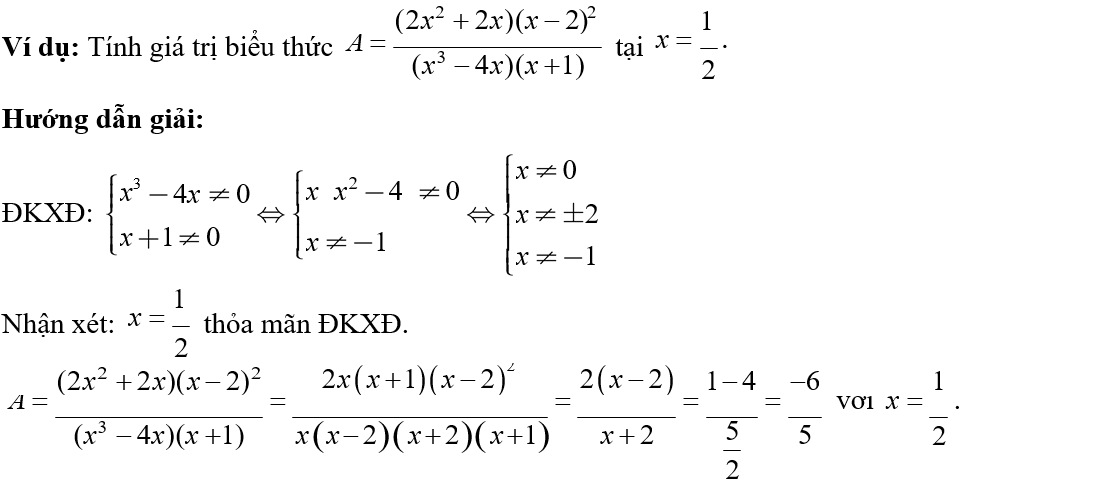
7. Bài toán tổng hợp

Phương pháp: Vận dụng các kĩ năng đã học để xử lý các ý của bài toán tổng hợp. Chú ý nếu đề bài chưa cho điều kiện của x thì việc đầu tiên cần làm là tìm điều kiện xác định và việc cuối cùng cần làm trong các bài toán tìm x là xét xem có thỏa mãn điều kiện xác định hay không, nếu không thỏa mãn thì loại.

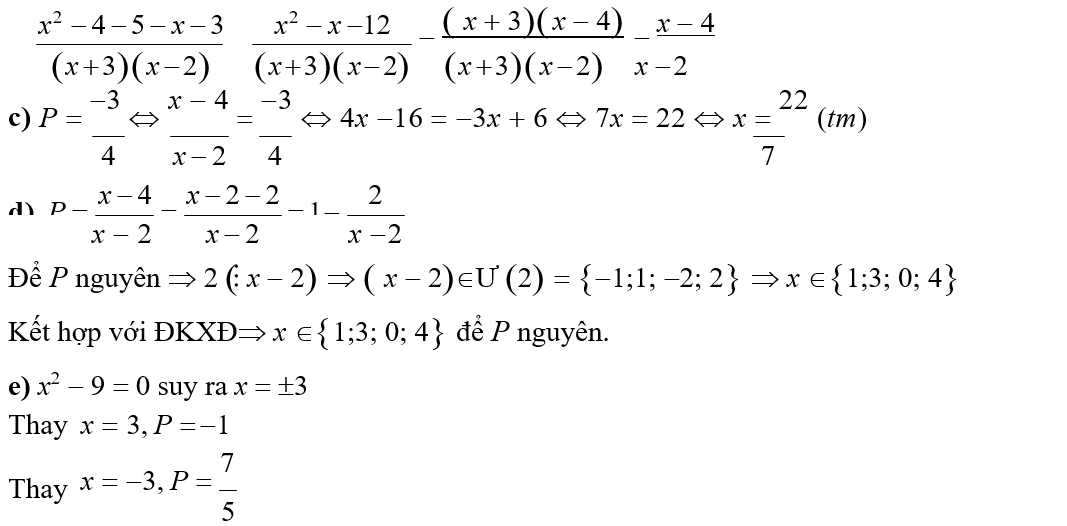
B. Hình học

1. Sử dụng tính chất của tứ giác để tính góc, tính độ dài cạnh

Phương pháp: Ghi nhớ các tính chất về tổng các góc trong một tứ giác, các tính chất đặc biệt của từng loại tứ giác đặc biệt, tính chất đường trung bình từ đó áp dụng vào việc tính góc, tính độ dài cạnh.

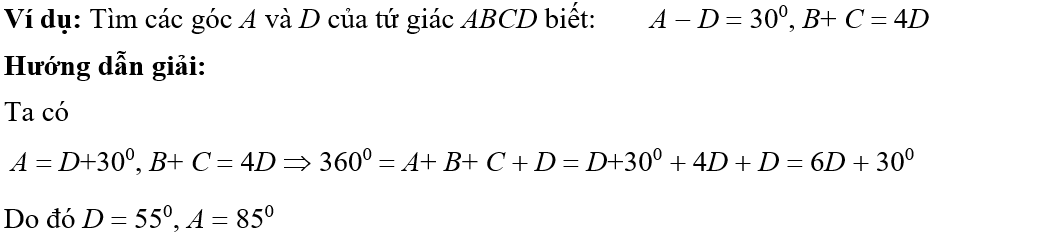
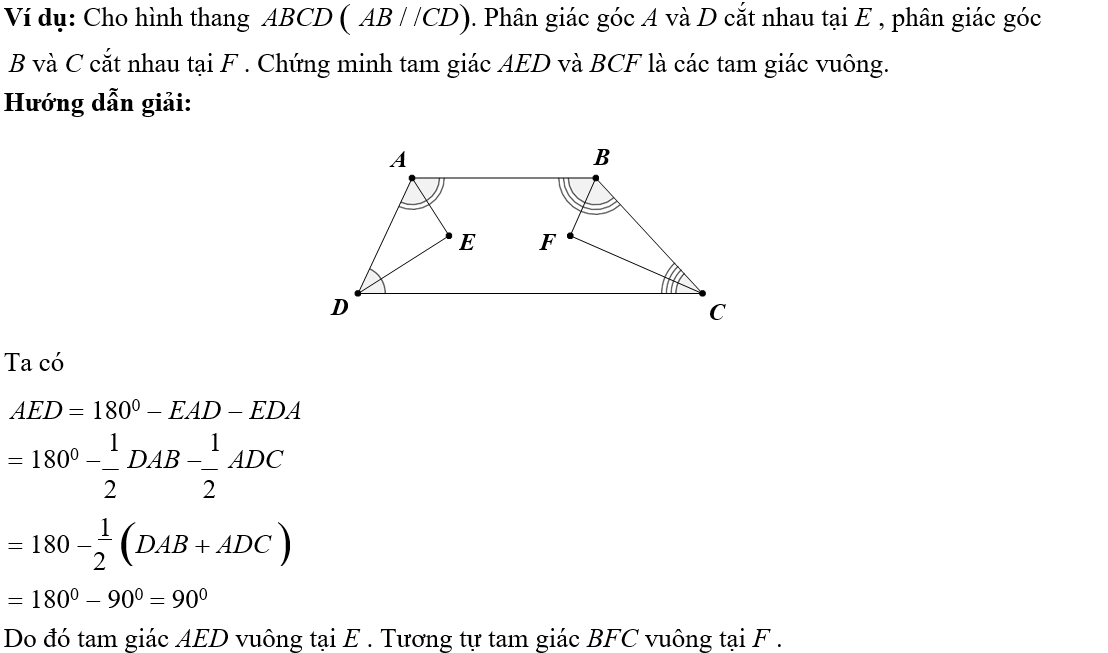
2. Chứng minh các tính chất, định lý dựa vào tính chất của tứ giác đặc biệt

Phương pháp: Ghi nhớ các tính chất đặc biệt của từng loại tứ giác đặc biệt để vận dụng vào việc lập luận chứng minh.

3. Sử dụng dấu hiệu nhận biết để chứng minh tứ giác là tứ giác đặc biệt

Phương pháp: Ghi nhớ dấu hiệu nhận biết của các loại tứ giác đặc biệt để áp dụng vào việc chứng minh tứ giác là tứ giác đặc biệt.

4. Tính số đo các góc của đa giác đều

Phương pháp: Đa giác đều n – cạnh có:

5. Tính số đường chéo của đa giác

Phương pháp: Đa giác n – cạnh có số đường chéo là: {n.(n-3)}/2

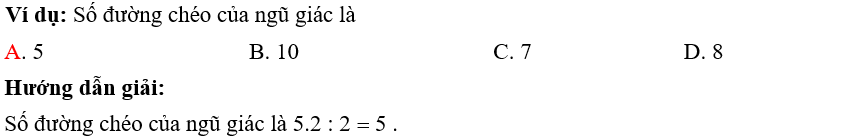
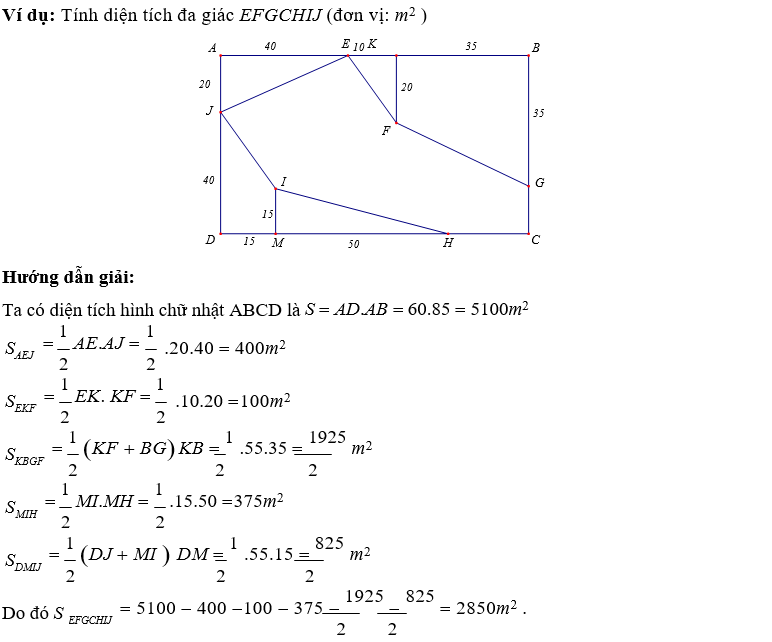
6. Tính diện tích đa giác

Phương pháp: Nếu đa giác đã cho không ở dạng các hình đã biết công thức diện tích thì ta có thể:

– Chia đa giác đã cho thành các đa giác nhỏ rồi cộng tổng diện tích các đa giác nhỏ.

– Tính diện tích phần bù: lấy diện tích đa giác chứa đa giác đã cho rồi trừ đi phần diện tích không thuộc đã giác đã cho.

→ Tham khảo chi tiết Đề cương ôn thi học kì 1 môn toán lớp 8 ngay tại đây (↓):

 

III – Tham khảo một số đề ôn thi học kì 1 lớp 8 môn toán

Đề ôn thi học kì 1 lớp 8 môn toán – Đề số 1
 

Đề ôn thi học kì 1 lớp 8 môn toán – Đề số 2
 

Đề ôn thi học kì 1 lớp 8 môn toán – Đề số 3
 

→  Tham khảo 3 đề tự luyện thi học kì 1 lớp 8 môn toán ngay tại đây!

Tham khảo thêm đề cương ôn tập các môn khác:

• Ôn thi học kì 1 môn Văn lớp 8
• Ôn thi học kì 1 môn Lý lớp 8
• Ôn thi học kì 1 môn Hóa lớp 8

 

Đề cương Ôn thi học kì 1 môn Toán lớp 8 trên đây là bài viết hệ thống lại toàn bộ những kiến thức mà các em học sinh đã được học ở trong chương trình môn Toán học kì I lớp 8. Hãy tham khảo thật kĩ, ôn tập và luyện tập nhiều đề để chuẩn bị được tốt nhất cho bài thi cuối học kì I sắp tới nhé!