Môn toán là một trong những môn học quan trọng nhất, được áp dụng, sử dụng trong mọi mặt của đời sống. Hàng ngày chúng ta đều phải thường xuyên tiếp xúc với những con số, những phép tính và những công thức toán học. Vậy nên, trong những kỳ thi lớn như kỳ thi học kỳ, những đề thi sẽ tương đối khó để cho các em có thể buộc phải nỗ lực hết mình. Bài viết dưới đây, HOCMAI đã tổng hợp kiến để ôn thi toán lớp 9 học kì 1, bao gồm đầy đủ lý thuyết và bài tập để giúp các em có thể dễ dàng vượt qua kỳ thi này hơn đấy.
I. Đề cương ôn tập toán 9 học kì 1
1. Đề cương Toán 9 Đại số Học kỳ 1
Gồm có 2 chương:
Chương 1: Căn bậc hai & căn bậc ba:
Chương 2: Hàm số bậc nhất:
- Hàm số bậc nhất.
- Đồ thị của hàm số bậc nhất.
- Vị trí tương đối của hai đường thẳng ( song song, cắt nhau, vuông góc, trùng nhau).
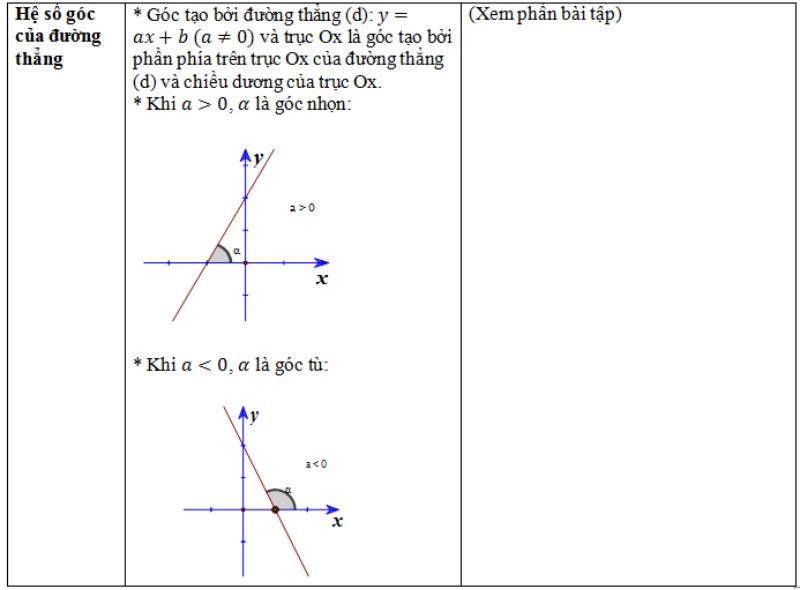
- Hệ số góc của đường thẳng.




2. Đề cương toán 9 phần hình học học kỳ 1
Gồm có 2 chương:
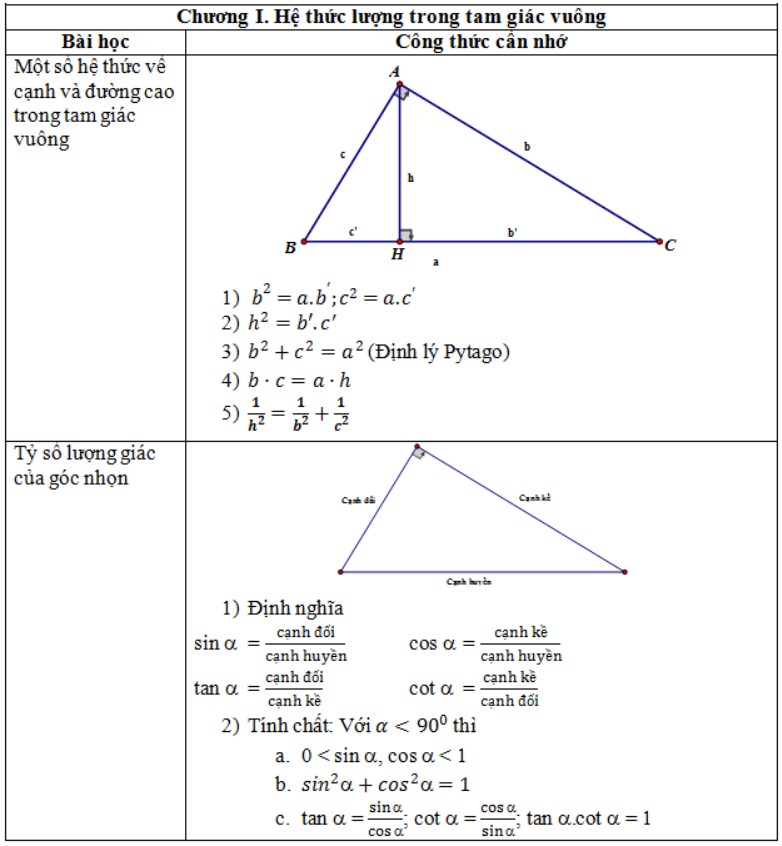
Chương 1: Hệ thức lượng trong một tam giác vuông:
- Hệ thức lượng giữa một cạnh và đường cao.
- Tỉ số lượng giác và công thức của một góc nhọn.
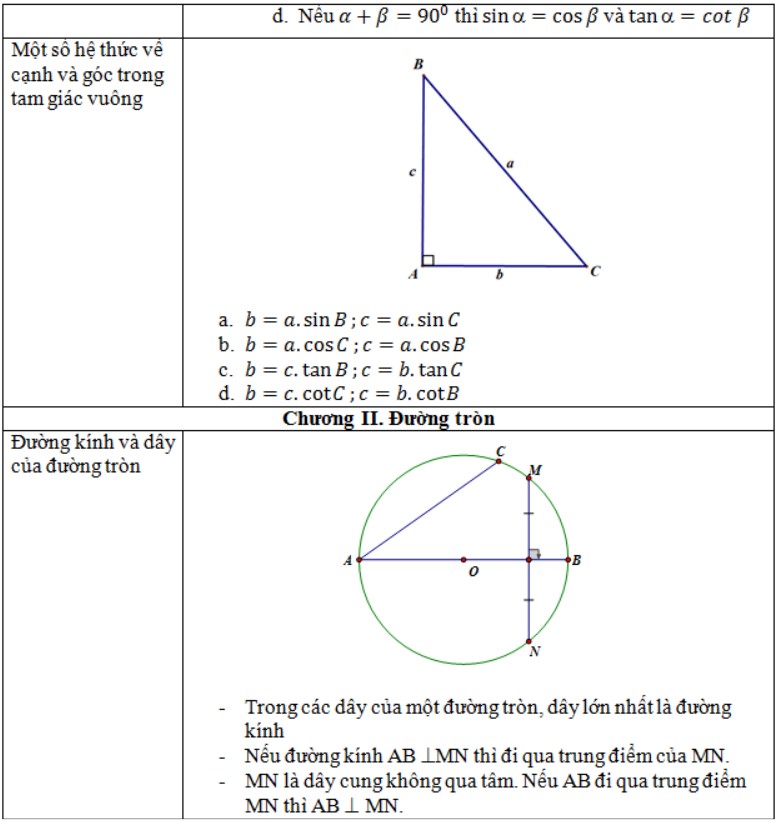
- Hệ thức lượng giữa một góc và một cạnh.
Chương 2: Đường tròn:
- Đường kính và dây cung.
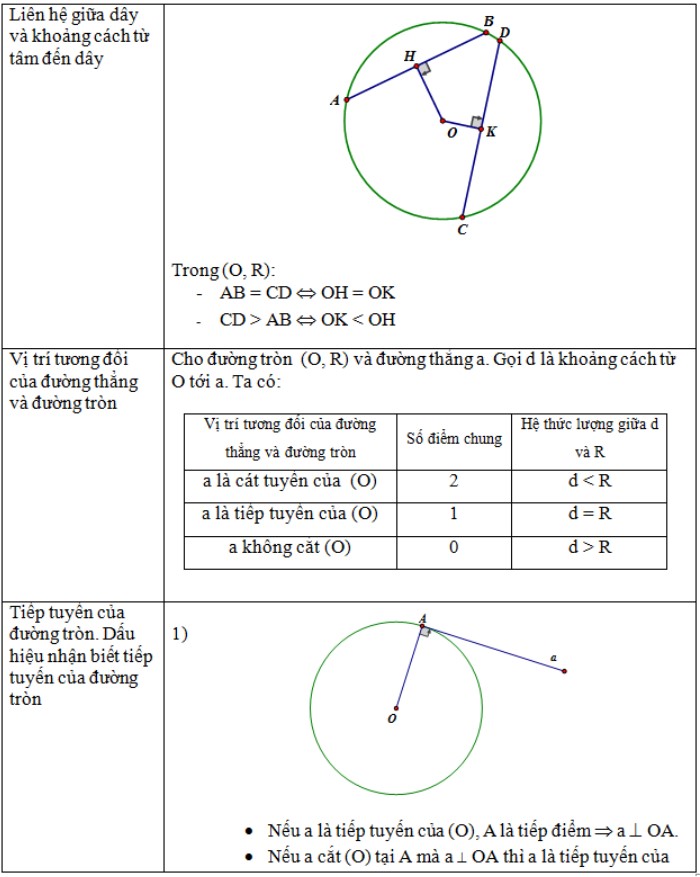
- Liên hệ giữa khoảng cách từ dây tới tâm và dây.
- Vị trí tương đối của một đường thẳng với một đường tròn.
- Tiếp tuyến của đường tròn.
- Vị trí tương đối của hai đường tròn với nhau.
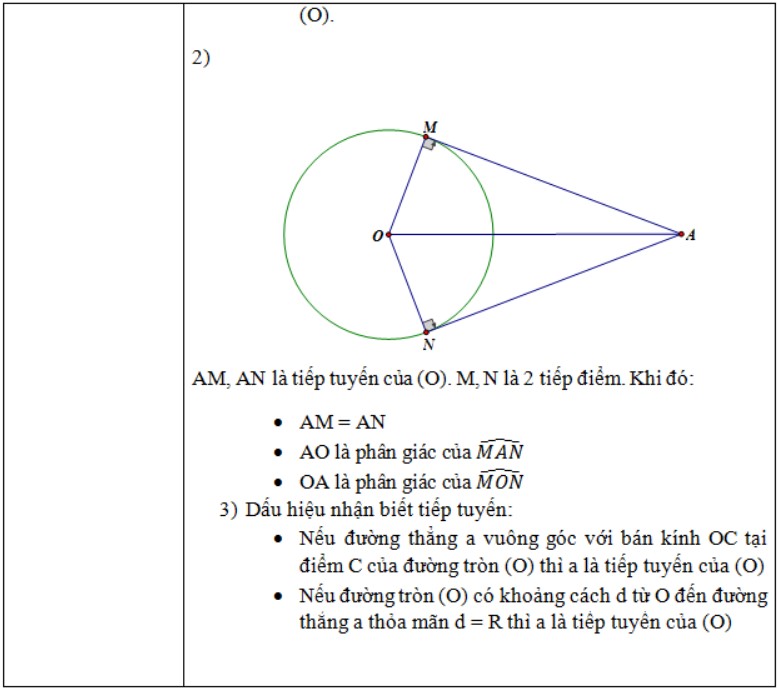
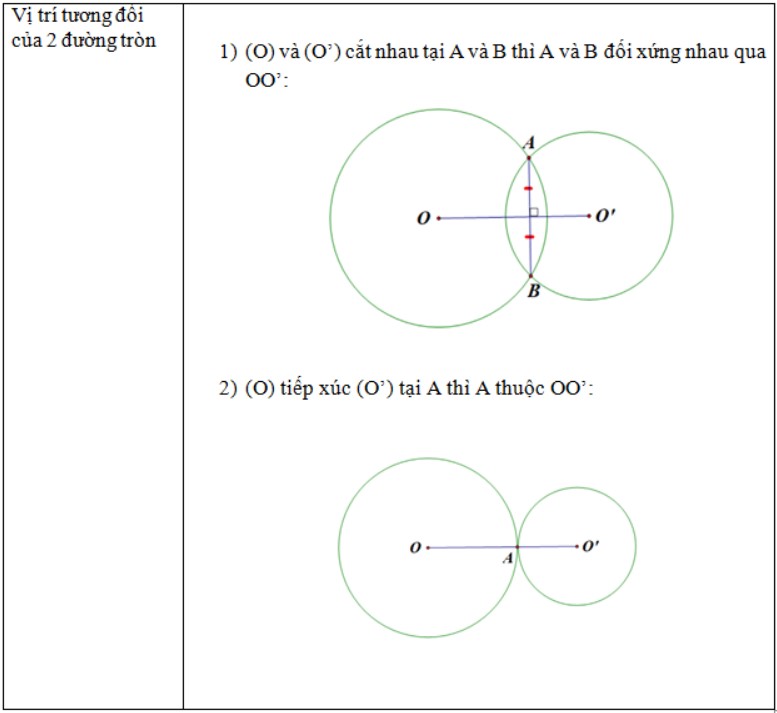
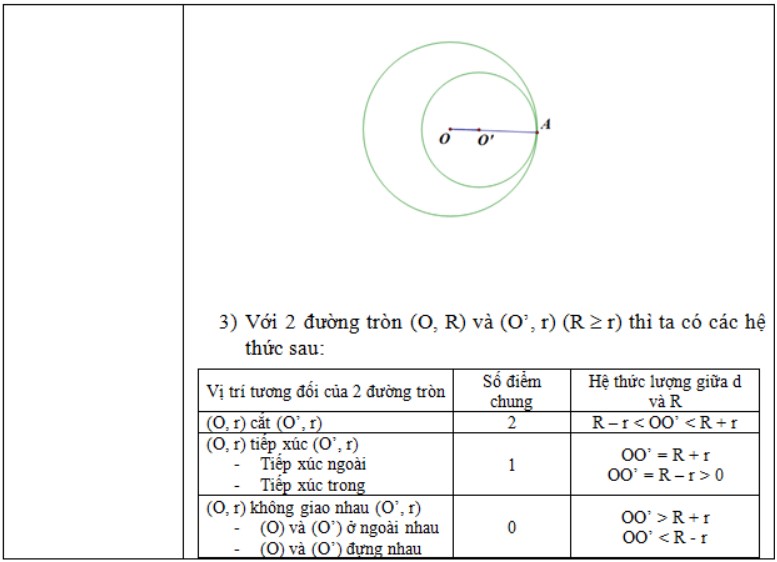
II. Một số câu hỏi ôn tập toán 9 học kì 1
1. Trắc nghiệm ôn thi học kì 1 lớp 9 môn toán
Câu 1: Cho một đường thẳng là y = (m + 5)x – 2. Đường thẳng này thì tạo một góc bằng 90 độ với đường thẳng x – 2y = 3 khi:
- A. m = -6
- B. m = -3
- C. m = -7
- D. m = -4
Câu 2: Cho một hàm số là: y = (m – 1)x + m – 1. Kết luận nào sau đây là kết luận đúng?
- A. Với giá trị m > 1 thì hàm số y là một hàm số đồng biến.
- B. Với giá trị m > 1 thì hàm số y là một hàm số nghịch biến.
- C. Với giá trị m = 0 thì đồ thị hàm số sẽ đi qua gốc tọa độ.
- D. Với giá trị m = 2 thì đồ thị hàm số sẽ đi qua điểm có tọa độ
Câu 3: Cho tam giác ABC có số đo của góc A bằng 90 độ, kẻ một đường cao AH. Biết rằng AC = 7, AB = 5; BH = x, CH = y. Chỉ ra một hệ thức sai trong những hệ thức sau:
- A. 5² = x²(x + y)²
- B. 5² = x(x + y)
- C. 7² = y(x + y)
- D. 5² + 7² = (x + y)²
Câu 4: Đề cho cosα = 0,8. Hãy tính sinα ( với α là một góc nhọn)
- A. sinα = 0,6
- B. sinα = ±0,6
- C. sinα = 0,4
- D. Kết quả khác
Câu 5: Cho cả hai đường thẳng xy và x’y’ giao với nhau và vuông góc với nhau tại O. Cho thêm một đoạn thẳng AB = 8 chuyển động sao cho điểm A thì luôn nằm trên đường xy và điểm B thì luôn nằm trên x’y’. Khi đó trung điểm M của đoạn AB thì sẽ di chuyển trên đoạn nào?
- A. Đường thẳng mà song song với đường xy và cách đường xy một đoạn là 4
- B. Đường thẳng mà song song với đường x’y’ và cách đường x’y’ một đoạn là 4
- C. Đường tròn tâm O với bán kính là 4
- D. Đường tròn tâm O với bán kính là 8
Câu 6: Với giá trị nào dưới đây của x thì biểu thức 9x² + 6x + 1 xác định có căn bậc hai? Câu nào sau đây là đáp án đúng nhất?
- A. Với mọi x > 0
- B. Với mọi x
- C. x = 0
- D. x = −13
Câu 7: Nếu có cho đồ thị y = mx + 2 song song với đồ thị y = -2x + 1 thì:
- A. Đồ thị hàm số y = mx + 2 sẽ cắt trục tung tại điểm có tung độ bằng 1
- B. Đồ thị hàm số y = mx + 2 sẽ cắt trục hoành tại điểm có hoành độ bằng 2
- C. Hàm số y = mx + 2 làm hàm số đồng biến
- D. Hàm số y = mx + 2 làm hàm số nghịch biến
Câu 8: Bộ ba nào ở bên dưới đây không phải là độ dài 3 cạnh của một tam giác vuông?
- A. (6; 8; 10)
- B. (7; 24; 25)
- C.(2–√,3–√,5–√)
- D.(13,14,15)
Câu 9: Ta cho đường tròn (O; 25). Khi đó dây lớn nhất của đường tròn (O; 25) có độ dài là bằng:
- A. 12,5
- B. 25
- C. 50
- D. 20
Câu 10: Đường tròn là một hình:
- A. Không có trục đối xứng
- B. Có một trục đối xứng
- C. Có hai trục đối xứng
- D. Có vô số trục đối xứng
Câu 11: Cho tam giác ABC. Biết rằng số đo ba cạnh lần lượt như sau:AB = 21, AC = 28, BC = 35. Tam giác ABC chính là tam giác gì?
- A. Tam giác này cân tại A
- B. Tam giác này vuông ở A
- C. Tam giác này là tam giác thường
- D. Cả 3 đều sai.
Câu 12: Cho một đường tròn là đường tròn (O; 15cm) có một dây AB = 24 cm thì khoảng cách từ tâm O đến dây AB đó là:
- A. 12 cm
- B. 9 cm
- C. 8 cm
- D. 6 cm
Câu 13: Cho một đường thẳng (k1): y = 4x – 5; (k2): y = 3x – 5. Đường thẳng (k1) nếu cắt đường thẳng (k2) thì tọa độ giao điểm của hai đường là:
- A. M(-5; 0)
- B. N(0; 5)
- C. P(0; -5)
- D. Q(5; 0)
Câu 14: Cho một tam giác ABC có đoạn BH và đoạn CE là hai đường cao. Gọi M là một giao điểm của đoạn BH và đoạn CE. I là trung điểm của đoạn BC. Khi đó lần lượt những điểm B, C, E, H cùng thuộc một đường tròn nào?
- A. (I; R = IA)
- B. (I; R = IB)
- C. (M; R = MB)
- D. (M; R = MA)
Câu 15: Gọi d là khoảng cách giữa hai tâm của hai đường tròn là đường tròn (O, R) và đường tròn (O’, r) (biết rằng 0 < r < R). Nếu để (O) và (O’) ở ngoài nhau thì số đo của d sẽ là:
- A. d < R – r
- B. d = R – r
- C. d = R + r
- D. d > R + r
2. Tự luận đề ôn thi toán lớp 9 học kì 1
Bài 1: Thực hiện các phép tính:
a) 4√24 – 3√54 + 5√6 – √150
b) 2/(3 + 2√2) – 2/(3 – √8)
c) √[(3√5 – 1)/(2√5 + 3)] – √[(√5 + 11)/(7 – 2√5)]
Hướng dẫn giải bài:
a) 4√24 – 3√54 + 5√6 – √150
= 8√6 – 9√6 + 5√6 – 5√6
= -√6
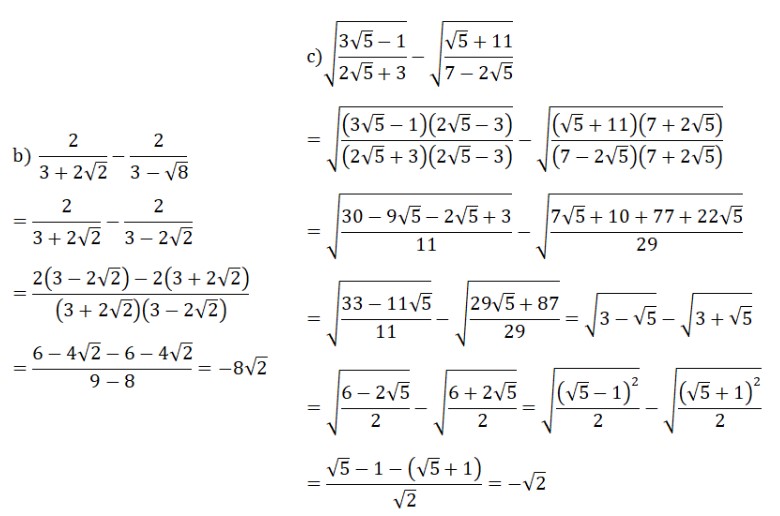
Bài 2: Vẽ cùng trên cùng một mặt phẳng tọa độ Oxy thì là đồ thị của các hàm số sau:
y = (-1/2) (d1) và y = (1/2)x + 3 (d2)
Xác định b để cho đường thẳng (d3) y = 2x + b cắt (d2) tại một điểm có hoành độ và tung độ sẽ đối nhau.
Hướng dẫn trả lời:
a) Tập xác định của hàm số R:
Bảng giá trị
| x | 0 | 2 |
| y = -1/2 x | 0 | – 1 |
| y = 1/2 x + 3 | 3 | 4 |
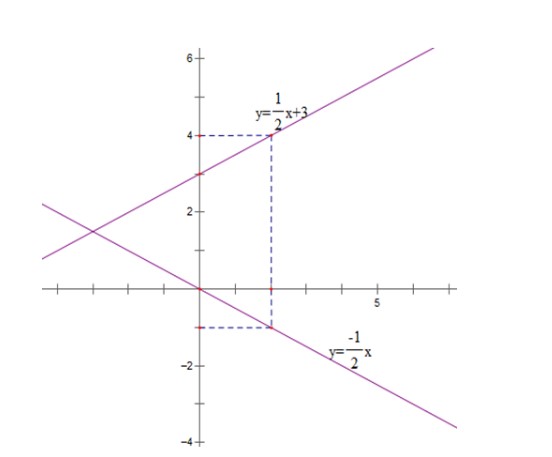
b) Gọi A (m; – m) là một tọa độ giao điểm của đường (d2) và đường (d3)
Khi đó:
-m = 1/2 m + 3 ⇔ 3/2 m = 3 ⇔ m = 2
Vậy tọa độ giao điểm của đường d2 và đường d3 là (2; -2)
⇒ -2 = 2.2 + b ⇔ b = -6
Vậy b = – 6
Bài 3: Giải phương trình:
√(x² – 4x + 4) = x + 2
Hướng dẫn giải bài:
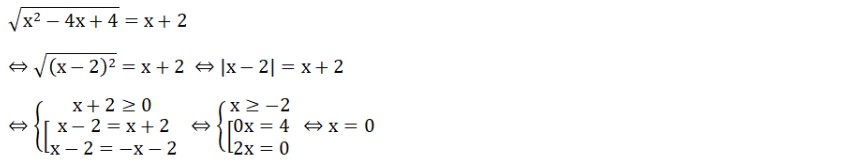
Vậy phương trình trên đã có nghiệm x = 0.
Bài 4: Cho biểu thức:
M = [(√x + 2)/(√x – 3)] – [(√x + 1)/(√x – 2)] – 3.[(√x – 1)/(x – 5√x + 6)] với x ≥ 0, x ≠ 4, x ≠ 9
a) Em hãy thu gọn biểu thức M.
b) Tìm giá trị của x để sao cho M < -1
Hướng dẫn giải bài:
a) Rút gọn M
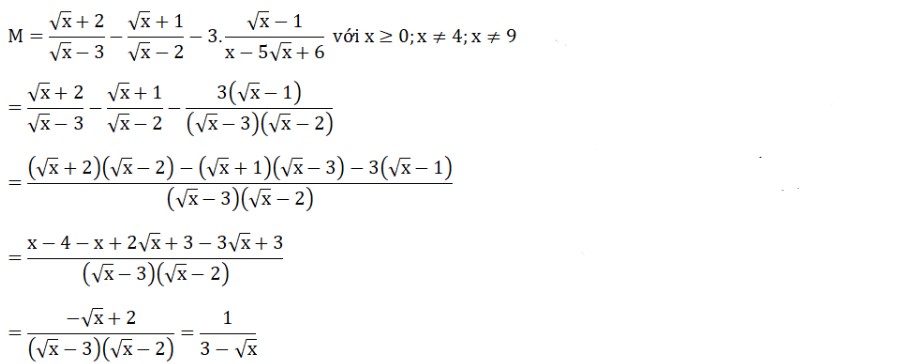
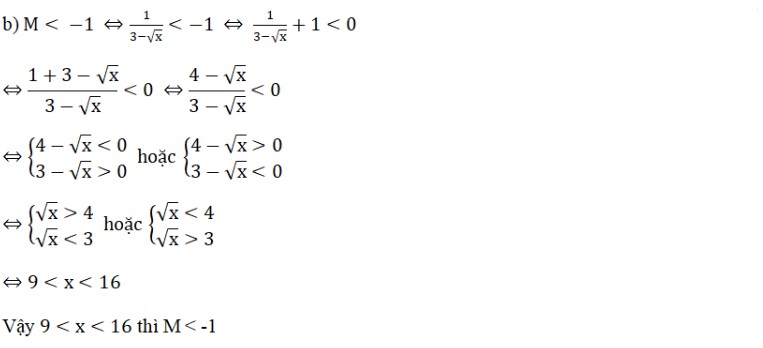
Bài 5: Cho một đường tròn tâm điểm O và bán kính là R (O;R) và một điểm M nằm ở ngoài đường tròn sao cho có đoạn OM = 8/5R. Kẻ các tiếp tuyến là MA và MB với đường tròn tâm O đó (sao cho điểm A và điểm B chính là hai tiếp điểm đó), đường thẳng AB cắt đoạn OM tại giao điểm là điểm K.
a) Chứng minh rằng độ dài AK và BK bằng nhau, nói cách khác là điểm K chính là trung điểm của đoạn thẳng AB.
b) Tính MA, OK, AB theo số đo R.
c) Kẻ lên đường kính AN của đường tròn tâm O đó. Kẻ đoạn BH vuông góc với AN tại điểm H. Chứng minh rằng MB.BN = BH.MO.
d) Đường thẳng MO cắt đường tròn (O) tại điểm C và điểm D (điểm C nằm giữa điểm O và điểm M). Gọi điểm E là điểm đối xứng của điểm C qua điểm K. Chứng minh rằng điểm E là trực tâm của tam giác ABD.
Hướng dẫn giải bài:

a) Ta có:
MA = MB (theo tính chất hai tiếp tuyến cắt nhau)
OA = OB (có độ dài cùng bằng bán kính đường tròn tâm O (O))
⇒ OM chính là đường trung trực của AB.
OM ∩ AB = K ⇒ điểm K là trung điểm của AB
b) Tam giác MAO vuông tại điểm A, đoạn AK là đường cao có:
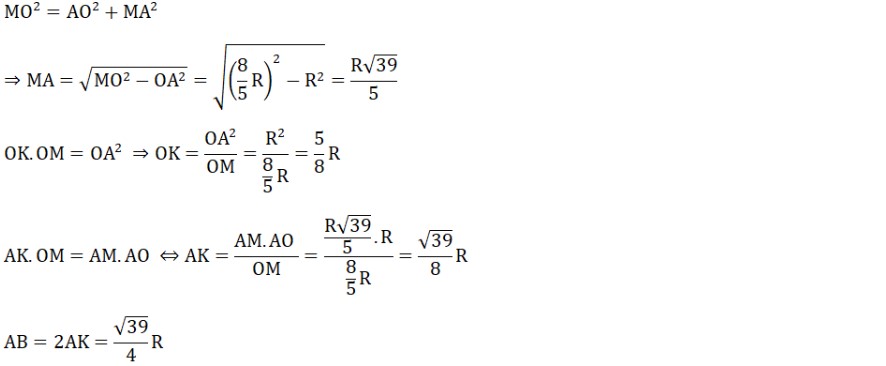
c) Ta có: góc ABN bằng 90 độ (điểm B nằm trên đường tròn đường kính AN)
⇒ BN // MO (vì cùng vuông góc với AB)
Do đó:
Góc AOM = góc ANB (vì đồng vị)
Góc AOM = góc BOM (vì đoạn OM là phân giác của góc AOB)
⇒ góc ANB = góc BOM
Xét ΔBHN và ΔMBO có:
góc BHN = góc MBO = 90o
góc ANB = góc BOM
⇒ ΔBHN ∼ ΔMBO (g.g)
⇒ BH/MB = BN/MO
Hay MB.BN = BH.MO
d) Ta có:
Điểm K là trung điểm của đoạn CE (điểm E đối xứng với điểm C qua đoạn AB)
Điểm K là trung điểm của đoạn AB
AB ⊥ CE (vì MO ⊥ AB)
⇒ Tứ giác AEBC là một hình thoi.
⇒ BE // AC
Mà AC ⊥ AD (điểm A thuộc đường tròn đường kính CD)
Nên DK ⊥ AB và BE ⊥ AD
Vậy điểm E là trực tâm của tam giác ADB
III. Bộ đề thi ôn tập toán 9 học kì 1 mới nhất
Chi tiết về cấu trúc/ ma trận đề thi học kì 1 Toán 9 chi tiết như sau:
| Cấp độ Chủ đề | Nhận biết | Thông hiểu | Vận dụng | Cộng | |
| Cấp độ thấp | Cấp độ cao | ||||
| 1. Căn thức bậc hai | – Xác định điều kiện có nghĩa của căn bậc hai. | – Hiểu được hằng đẳng thức để rút gọn biểu thức | Vận dụng các phép biến đổi đơn giản để rút gọn, tính giá trị biểu thức | Vận dụng các phép biến đổi để rút gọn được biểu thức phức tạp, giải phương trình vô tỷ | |
| Số câu:2 Số điểm:1 |
Số câu:2 Số điểm:1 |
Số câu:2 Số điểm: 1. |
Số câu:1 Số điểm:0,5 |
Số câu: 7 Số điểm:3.5 |
|
| 2. Hàm số bậc nhất | Nhận biết được hàm số đồng biến hoặc nghịch biến | Hiểu được hai đường thẳng song song,… Vẽ được đồ thị hàm số |
Tìm được giao điểm đồ thị của hai hàm số bậc nhất | ||
| Số câu:2 Số điểm:1 |
Số câu:2 Số điểm:1 |
Số câu:2 Số điểm:1 |
Số câu: 6 Số điểm: 3 |
||
| 3. Hệ thức lượng trong tam giác vuông. | Hiểu được các hệ thức áp dụng vào tam giác vuông | Vận dụng các hệ thức lượng ở trong tam giác vuông để giải toán | |||
| Số câu:1 Số điểm:0.5 |
Số câu:1 Số điểm:0.5 |
Số câu: 2 Số điểm: 1.0 |
|||
| 4. Đường tròn | Nhận biết được đường tròn | Hiểu được tính chất đường tròn, hai tiếp tuyến cắt nhau để chứng minh | Vận dụng khái niệm đường tròn và những tính chất đường tròn, hai tiếp tuyến cắt nhau của đường tròn để chứng minh | ||
| Số câu:1 Số điểm: 05 |
Số câu:1 Sốđiểm:0.5 |
Số câu:2 Số điểm 1 |
Số câu:1 Số điểm:0.5 |
Số câu: 5 Số điểm:3 |
|
| Tổng | Số câu:4 Số điểm: 2.0 |
Số câu: 7 Số điểm: 3.5 |
Số câu:8 Số điểm: 4.0 |
Số câu: 2 Số điểm: 1.0 |
Số câu: 20 Số điểm: 10 |
Sau đây là tổng hợp bộ tài liệu gồm 10 đề thi học kỳ I Toán 9 có lời giải chi tiết do HOCMAI tổng hợp. Để sử dụng bộ tài liệu tốt nhất, các bạn hãy photo ra giấy rồi thực hành trực tiếp nhé!
Vậy là các em học sinh khối 9 thân thương đã nắm rõ được những kiến thức trọng tâm mà mình cần nắm vững và làm những bài tập này thật nhuần nhuyễn chưa nhỉ? Với những kiến thức trong bài viết ôn thi toán lớp 9 học kì 1 này, các em có thể vững tin làm được thật nhiều bài tập khác nhau, kể cả trong sách giáo khoa và kể cả các bài tập nâng cao mà thầy cô giáo giao ở trên lớp nữa đấy. Các em hãy tìm thêm thật nhiều kiến thức bổ ích nữa tại hoctot.hocmai.vn nhé!
















