Đề cương ôn thi học kì 2 toán 9 đầy đủ, chi tiết nhất

Bài viết này là bài Đề cương ôn thi học kì 2 toán 9 đầy đủ và chi tiết nhất, dành cho các em học sinh khối 9 đang trong quá trình ôn thi cuối kì môn toán. Bài đề cương này đã được HOCMAI tổng hợp đầy đủ kiến thức trọng tâm và bài tập vận dụng. Các em hãy ôn luyện chăm chỉ nhé!

A. LÝ THUYẾT MÔN TOÁN LỚP 9 HỌC KÌ 2

I. Đề cương ôn tập toán 9 học kì 2 – Phần Đại số

Chương 3 → Hệ hai phương trình bậc nhất có hai ẩn

 

• Bài 1 → Phương trình bậc nhất có hai ẩn số

• Bài 2 → Hệ hai phương trình bậc nhất có hai ẩn số

• Bài 3 → Giải hệ phương trình cùng với phương pháp thế

• Bài 4 → Giải hệ phương trình cùng với phương pháp cộng đại số

• Bài 5 + 6 → Giải bài toán với cách lập hệ phương trình

 

Chương 4 → Hàm số y = ax² với a khác 0 – Phương trình bậc 2 có một ẩn

 

• Bài 1 → Hàm số y = ax² với a khác 0

• Bài 2 → Đồ thị hàm số y = ax² với a khác 0

• Bài 3 → Phương trình bậc hai có một ẩn số

• Bài 4 → Công thức tính nghiệm của phương trình bậc hai

• Bài 5 → Công thức tính nghiệm dạng thức thu gọn

• Bài 6 → Hệ thức Vi – ét và những ứng dụng của chúng

• Bài 7 → Phương trình được quy về dạng thức phương trình bậc hai

• Bài 8 → Giải bài toán với phương pháp lập phương trình.

 

II. Lý thuyết toán hình 9 học kì 2

Chương 3 → Góc với đường tròn

 

• Bài 1 → Tính số đo cung và góc ở tâm

• Bài 2 → Liên hệ giữa dây của cung và cung đó

• Bài 3 → Góc nội tiếp

• Bài 4 → Góc được tạo bởi tia tiếp tuyến với dây cung

• Bài 5 → Góc có đỉnh nằm bên trong đường tròn và góc có đỉnh nằm bên ngoài đường tròn

• Bài 6 → Cung có chứa góc

• Bài 7 → Tứ giác nội tiếp đường tròn

• Bài 8 → Đường tròn ngoại tiếp và đường tròn nội tiếp

• Bài 9 → Độ dài của đường tròn và cung tròn

• Bài 10 → Diện tích của hình tròn và diện tích của quạt tròn.

 

Chương 4 → Hình trụ – Hình nón – Hình cầu

 

• Bài 1 → Hình trụ – Tính diện tích xung quanh của hình trụ và thể tích của hình trụ

• Bài 2 → Hình nón – Hình nón cụt – Tính diện tích xung quanh của hình nón, hình nón cụt và thể tích của hình nón, hình nón cụt.

• Bài 3 → Hình cầu – Tính diện tích của mặt cầu và thể tích của hình cầu.

 

B. TỔNG HỢP KIẾN THỨC ÔN TẬP THI HỌC KÌ 2 TOÁN 9

I. KIẾN THỨC TOÁN ĐẠI LỚP 9 HỌC KÌ 2

1. Chương 3 → Hệ hai phương trình bậc nhất có hai ẩn

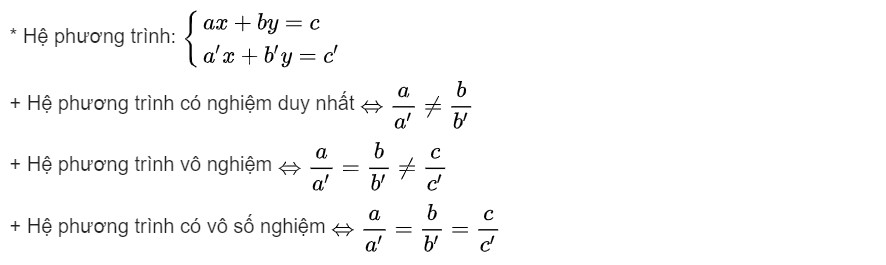
* Giải bài toán bằng phương pháp tạo lập phương trình, lập hệ phương trình.

+ Bước 1 → Tạo lập phương trình hoặc tạo lập hệ phương trình.

+ Bước 2 → Giải hệ phương trình hoặc giải phương trình.

+ Bước 3 → Kiểm tra những nghiệm của phương trình hoặc của hệ phương trình xem nghiệm nào thích hợp sau đó kết luận.

2. Chương 4 → Phương trình bậc hai một ẩn

Phương trình ax²  + bx + c = 0 (a ≠ 0)

* Hàm số y = ax²  (a ≠ 0) có tính chất:

+ Nếu khi a > 0, hàm số nghịch biến khi có x < 0 và đồng biến khi có x > 0.

+ Nếu khi a < 0, hàm số đồng biến khi x < 0 và nghịch biến khi x > 0.

* Hàm số y = ax²  (a ≠ 0) này là một đường cong parabol chắc chắn đi qua gốc tọa độ O (0;0)

+ Nếu khi a > 0 thì đồ thị sẽ nằm phía trên của trục hoành.

+ Nếu khi a < 0 thì đồ thị sẽ nằm phía dưới của trục hoành.

* Vị trí tương đối của đường thẳng xét so với đường cong parabol là: Xét đường thẳng y = ax + b (d) và đường cong y = ax² (P)

+ TH (d) và (P) giao nhau ở tại hai điểm, khi phương trình hoành độ giao điểm cùng tạo bởi đường cong và đường thẳng có hai nghiệm phân biệt.

+ TH (d) tiếp xúc với (P) ở tại một điểm, khi phương trình hoành độ giao điểm cùng tạo bởi đường cong và đường thẳng có nghiệm kép.

+ TH (d) không giao (P), khi phương trình hoành độ giao điểm cùng tạo bởi đường cong và đường thẳng là vô nghiệm.

II. KIẾN THỨC TOÁN HÌNH LỚP 9 HỌC KÌ 2

1. Chương 2, 3 → Đường tròn | Góc với đường tròn

* Quan hệ vuông góc giữa dây và đường kính ở trong cùng một đường tròn:

+ Trong TH có một dây vuông góc với đường kính → thì đường kính sẽ qua trung điểm của dây đó.

+ Trong TH đường kính giao với một dây tại trung điểm của dây đó (dây không đi qua tâm) → thì đường kính sẽ vuông góc với dây đó.

* Liên hệ giữa khoảng cách từ tâm đến với một dây và dây đó ở trong cùng một đường tròn:

+ Hai dây bằng nhau → thì cách đều tâm.

+ Hai dây cách đều tâm → thì bằng nhau.

+ Dây nào lớn hơn → thì dây đó gần tâm hơn.

+ Dây nào gần tâm hơn → thì dây đó lớn hơn.

* Liên hệ giữa dây với cung: ở trong một đường tròn hoặc ở trong hai đường tròn bằng nhau:

+ Hai cung bằng nhau → căng hai dây bằng nhau.

+ Hai dây bằng nhau → căng hai cung bằng nhau.

+ Cung lớn hơn → căng dây lớn hơn.

+ Dây lớn hơn → căng cung lớn hơn.

* Tiếp tuyến của đường tròn:

+ Tính chất của đường tiếp tuyến là: tiếp tuyến sẽ vuông góc với bán (đường kính) và đi qua một điểm gọi là tiếp điểm.

+ Dấu hiệu để nhận biết được tiếp tuyến:

– Đường thẳng tiếp tuyến và đường tròn chỉ có đúng một điểm chung.

+ Khoảng cách tính từ tâm của đường tròn đến đường thẳng tiếp tuyến bằng với độ dài bán kính.

+ Đường thẳng tiếp tuyến đi qua một điểm nằm ở trên đường tròn và vuông góc với bán kính giao qua điểm đó.

+ Tính chất của 2 tiếp tuyến giao nhau: nếu có MF, ME là hai tiếp tuyến giao nhau tại điểm M của một đường tròn thì:

– MF = ME

– Có O là tâm của đường tròn (O). MO là đường phân giác của góc FME và OM là đường phân giác của góc FOE.

* Góc với đường tròn:

+ Những góc nội tiếp số đo bằng nhau → chắn các cung bằng nhau.

+ Những góc nội tiếp cùng chắn với một cung → thì bằng nhau.

+ Những góc nội tiếp chắn những cung bằng nhau → thì bằng nhau.

+ Góc nội tiếp số đo nhỏ hơn hoặc bằng 90 độ → có số đo bằng nửa số đo của góc ở tâm cùng chắn với một cung.

+ Góc nội tiếp mà chắn nửa đường tròn → là một góc vuông. Ngược lại có góc vuông nội tiếp → thì sẽ chắn nửa đường tròn.

+ Góc được tạo bởi đường tiếp tuyến và dây cung sẽ có độ lớn bằng với góc nội tiếp cùng chắn một cung.

* Với l là độ dài của cung, R là bán kính đường tròn, C là độ dài của đường tròn thì:

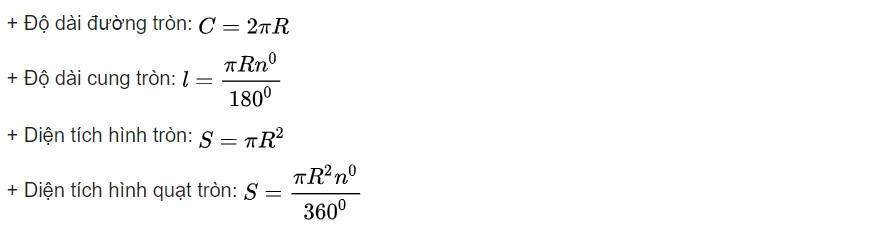
2. Chương 4 → Hình trụ | hình nón | hình cầu

* Với h (chiều cao) và l (đường sinh) thì:

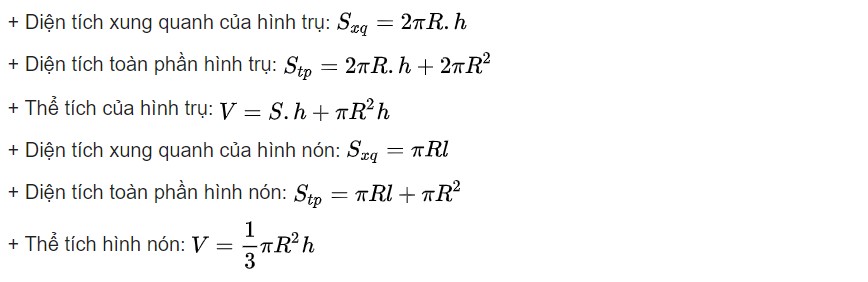
C. CÁC DẠNG BÀI TẬP TOÁN LỚP 9 ÔN THI HỌC KÌ 2

I. Ôn tập học kì 2 toán 9 – Phần đại số

1. Dạng toán căn bậc 2 và căn bậc 3 

• Rút gọn 
• Tinh giá trị biểu thức 
• Giải những phương trình, các bất phương trình để tìm ẩn x
• Những bài toán về giá trị nguyên 
• Những bài toán về GTNN và GTLN 

2. Hàm số bậc nhất và hàm số y = a x 2 (với a khác 0)

• Xác định những khoảng nghịch biến, khoảng đồng biến của hàm số.
• Tìm điều kiện của tham số để cho hàm số nghịch biến hoặc đồng biến trên một miền.
• Tìm điều kiện để hai đường thẳng ở vị trí giao nhau, trùng nhau hoặc song song nhau.
• Nhận biết được đồ thị hàm số .
• Cách thức xác định tọa độ của giao điểm của những đường thẳng.
• Tạo lập phương trình của đường thẳng.
• Tìm ra các điều kiện để đường thẳng giao đồ thị tại 2 điểm thỏa mãn được tính chất k.

3. Hệ 2 phương trình bậc nhất có 2 ẩn 

• Giải hệ phương trình và giải bài toán bằng phương pháp lập phương trình hoặc lập hệ phương trình.

4. Phương trình bậc 2 có một ẩn

• Giải phương trình bậc hai và tìm ra điều kiện của tham số để phương trình đảm bảo tính chất a. 

II. Đề cương ôn tập cuối năm toán 9 – Phần toán hình

• Chứng minh nhiều điểm cùng nằm trên một đường tròn.
• Tính độ dài của đoạn thẳng, tính số đo góc, chứng minh được hệ thức hình học cùng một số những biểu thức liên quan.
• Bài toán liên quan tiếp tuyến đường tròn.
• Chứng minh rằng: hai đường thẳng song song, ba đường thẳng đồng quy, hai đường thẳng vuông góc.
• Cách để tính được diện tích, thể tích của hình trụ và hình cầu và hình nón,…

III. Bài tập tham khảo ôn thi học kì 2 toán 9

Câu 1: Giải các phương trình sau:

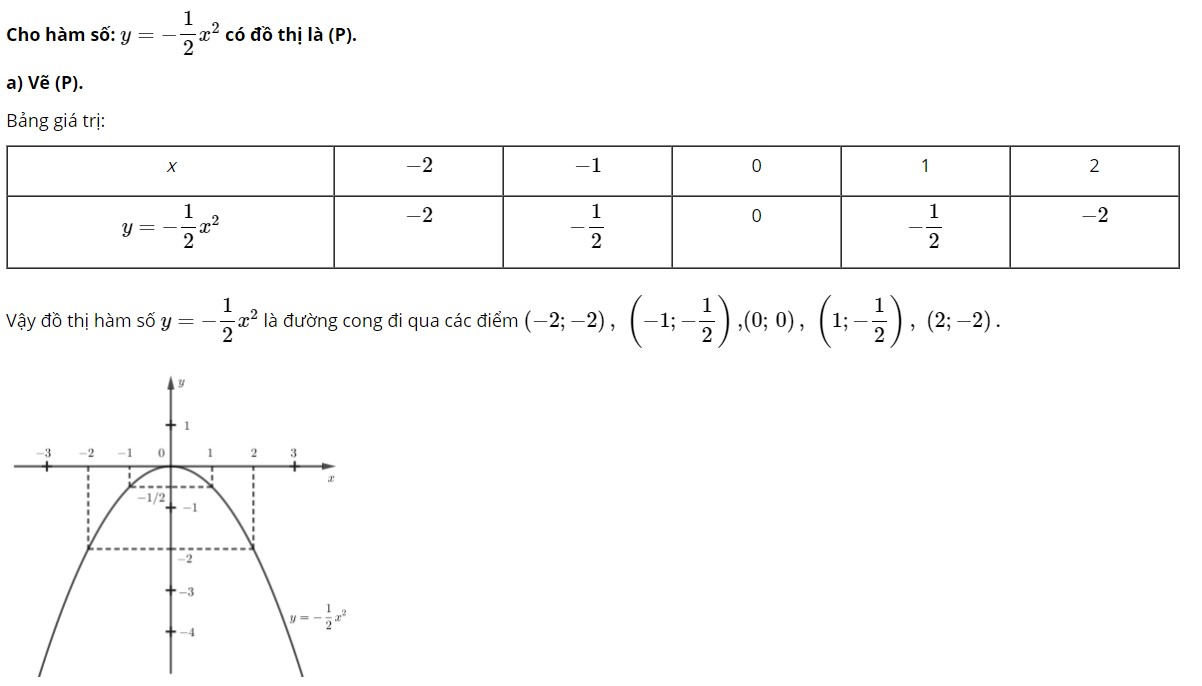
Câu 2: Cho hàm số: y = -1/2.x²  có đồ thị là (P).

a) Vẽ (P)

b) Tìm các tọa độ giao điểm của (P) và đường thẳng (D) y = x – 4 bằng phép toán

Câu 3: Một khu vườn hình chữ nhật có chu vi 70m. Tính diện tích khu vườn viết 2 lần chiều dài nhỏ hơn 3 lần chiều rộng 5m.

Câu 4: Một xí nghiệp may cần thanh lý 1410 bộ quần áo. Biết mỗi ngày xí nghiệp đó bán được 30 bộ quần áo. Gọi x là số ngày đã bán, y là số bộ quần áo còn lại sau x ngày bán.

a) Hãy lập công thức tính y theo x

b) Xí nghiệp cần bao nhiêu ngày để bán hết số quần áo cần thanh lý?

Câu 5: Cho A là điểm thuộc nửa đường tròn tâm (O) đường kính BC = 6cm và góc ACB = 30 độ. Tính AB, AC và diện tích phần tô đậm.

Câu 6: Cho phương trình x² – 2x + m = 0 (x là ẩn).

a) Tìm m để phương trình có hai nghiệm x1 và x2.

b) Gọi x1 và x2 là hai nghiệm của phương trình trên. Tìm m để:

Câu 7: Cho tam giác ABC nhọn (AB < AC) nội tiếp đường tròn tâm (O), các đường cao BE và CF cắt nhau tại H.

a) Chứng minh tứ giác AFHE và BFEC nội tiếp.

b) Hai đường thẳng EF và BC cắt nhau tại I. Vẽ tiếp tuyến ID với (O) (điểm D là tiếp điểm, D thuộc cung nhỏ BC). Chứng minh ID² = IB.IC

c) DE, DF cắt đường tròn (O) tại M và N. Chứng minh NM // EF.

Hướng dẫn giải bài:

Câu 1:

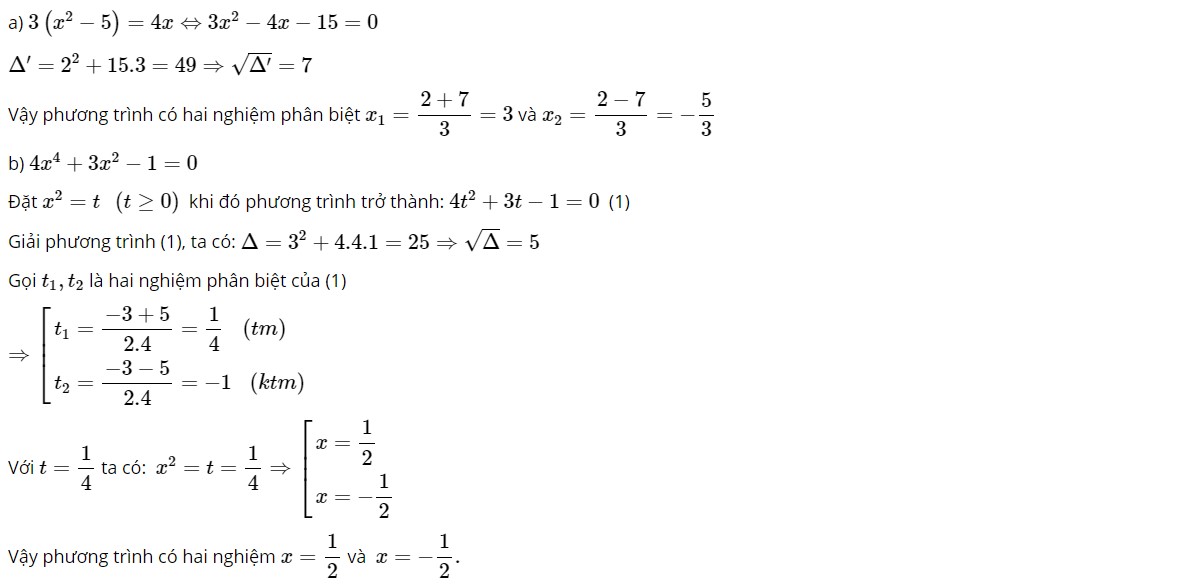
Câu 2:

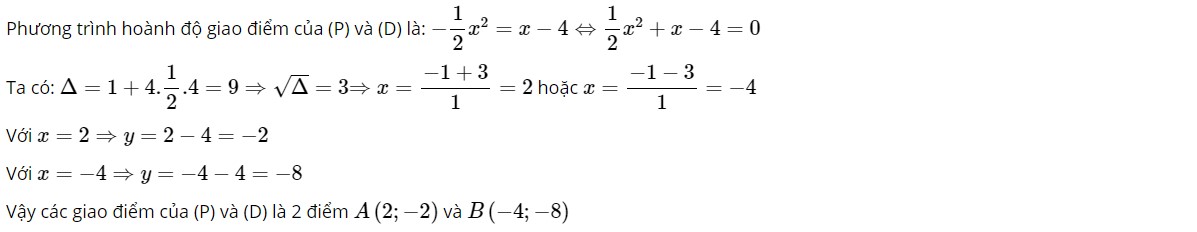
Câu 3:

Câu 4:

Câu 5:

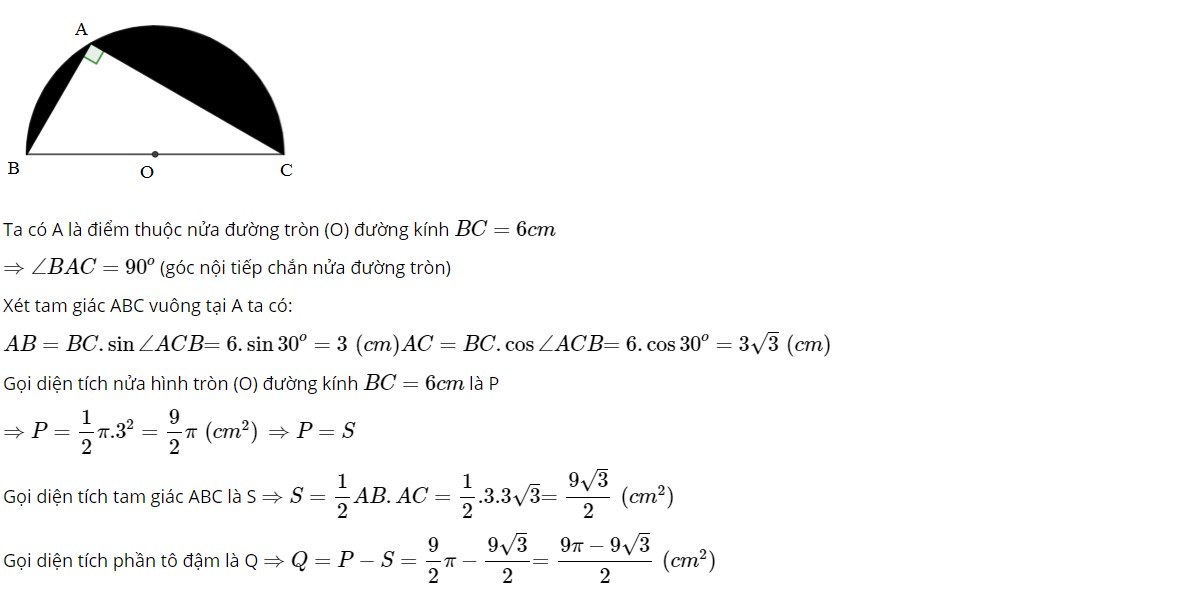
Câu 6:

Câu 7:

D. TỔNG HỢP ĐỀ THI HỌC KÌ 2 TOÁN 9 CÓ ĐÁP ÁN

Trên đây là bài viết Đề cương ôn thi học kì 2 toán 9 đầy đủ, chi tiết nhất mà HOCMAI gửi tới các em học sinh khối 9. Các em hãy chăm chỉ, luyện tập nhiều lần những bài tập, đề thi bên trên nhé. Chúc các em làm bài thi thật tốt, dành được điểm cao xứng đáng nhé!